题目内容
9.已知集合A=$\left\{{({x,y})|\frac{y-3}{x-2}=1}\right\},B=\left\{{({x,y})|y=ax+2}\right\}$,若A∩B=∅,则实数a的取值集合为{1,$\frac{1}{2}$}.分析 化简A={(x,y)|y=x+1,x≠2},从而可得y=x+1,(x≠2)与y=ax+2平行或y=ax+2过点(2,3),从而解得.
解答 解:A={(x,y)|y=x+1,x≠2},
B={(x,y)|y=ax+2};
∵A∩B=∅,
∴y=x+1,(x≠2)与y=ax+2平行或y=ax+2过点(2,3),
即a=1或3=2a+2,
解得,a=1或a=$\frac{1}{2}$;
故答案为:{1,$\frac{1}{2}$}.
点评 本题考查了集合的运算的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知向量$\overrightarrow a=(x,2)$与$\overrightarrow{b}$=(2,1)垂直,则$\overrightarrow a+2\overrightarrow b$与2$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
4.函数$f(x)={log_{\frac{1}{2}}}$cosx在x∈(0,2π)时的单调递增区间是( )
| A. | $({0,\frac{π}{2}})$ | B. | (0,π) | C. | (π,2π) | D. | $({\frac{3π}{2},2π})$ |
19.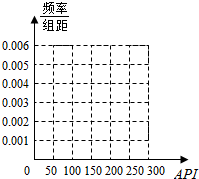 某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
(I)求频率分布表中①、②位置相应的数据,并完成频率分布直方图;
(Ⅱ)请由频率分布直方图来估计这100天API的平均值;
(Ⅲ)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为
S=$\left\{\begin{array}{l}{0,0≤ω≤100}\\{4ω-400,00<ω≤200}\\{4.8ω-600,200<ω≤300}\end{array}\right.$,若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不
超过600元的概率.
 某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:
某城市随机抽取一年内100天的空气质量指数API的监测数据,结果统计如下:| API | 空气质量 | 频数 | 频率 |
| [0,50] | 优 | 5 | 0.05 |
| [50,100] | 良 | ① | 0.2 |
| [100,150] | 轻度污染 | 25 | ② |
| [150,200] | 轻度污染 | 30 | 0.3 |
| [200,250] | 中度污染 | 10 | 0.1 |
| [250,300] | 中度重污染 | 10 | 0.1 |
| 合计 | 100 | 1.00 | |
(Ⅱ)请由频率分布直方图来估计这100天API的平均值;
(Ⅲ)假如企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为
S=$\left\{\begin{array}{l}{0,0≤ω≤100}\\{4ω-400,00<ω≤200}\\{4.8ω-600,200<ω≤300}\end{array}\right.$,若将频率视为概率,在本年内随机抽取一天,试估计这天的经济损失S不
超过600元的概率.
