题目内容
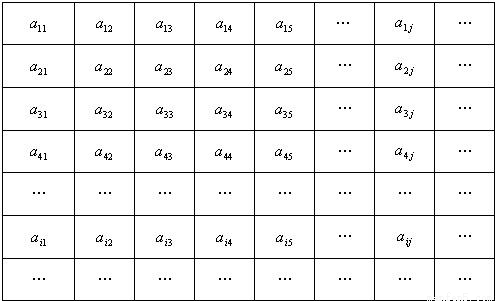
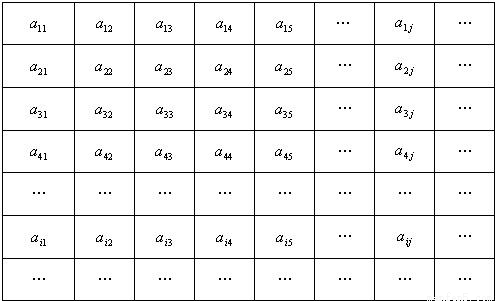
在下列由正数排成的数表中,每行上的数从左到右都成等比数列,并且所有公比都等于q,每列上的数从上到下都成等差数列.aij表示位于第i行第j列的数,其中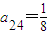 ,a42=1,
,a42=1,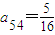 .
.
(Ⅰ)求q的值;
(Ⅱ)求aij的计算公式;
(Ⅲ)设数列{bn}满足bn=ann,{bn}的前n项和为Sn,试比较Sn与Tn=
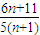 ( n∈N*)的大小,并说明理由.
( n∈N*)的大小,并说明理由.
【答案】分析:(Ⅰ)利用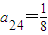 和
和 求出a44,再利用每行上的数从左到右都成等比数列,并且所有公比都等于q来求公比即可.
求出a44,再利用每行上的数从左到右都成等比数列,并且所有公比都等于q来求公比即可.
(Ⅱ)先求出ai4,然后在利用第i行成等比数列,且公比 ,即可求出aij的计算公式;
,即可求出aij的计算公式;
(Ⅲ)有(Ⅱ)的结论求出bn的通项,再利用错位相减法求出Sn,然后研究出Sn与Tn= 对应的函数的单调性,利用单调性来比较Sn与Tn=
对应的函数的单调性,利用单调性来比较Sn与Tn= 的大小即可.
的大小即可.
解答:解:(Ⅰ)设第4列公差为d,则 .
.
故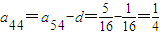 ,于是
,于是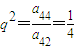 .
.
由于aij>0,所以q>0,故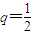 .(3分)
.(3分)
(Ⅱ)在第4列中, .
.
由于第i行成等比数列,且公比 ,
,
所以, .(6分)
.(6分)
(Ⅲ)由(Ⅱ)可知 .即bn=
.即bn= .
.
所以Sn=b1+b2+b3++bn=a11+a22+a33++ann.
即 ,
,
故 .
.
两式相减,得 =
= ,
,
所以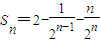 .(8分)
.(8分)
设f(x)=2-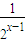 -
- (x>0),
(x>0),
即f(x)=2-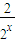 -
-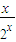 =2-
=2- =2-(2+x)2-x.
=2-(2+x)2-x.
因为f′(x)=-[2-x+(2+x)2-x(-1)ln2]=2-x[(2+x)ln2-1]
=2-x[ln22+x-lne]=2-xln ,
,
且当x>0时,x+2>2.所以22+x>22=4.
于是 >
> >1.
>1.
所以ln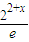 >0.
>0.
又2-x>0,
所以在(0,+∞)上f′(x)=2-xln >0.
>0.
因此函数f(x)=2- -
-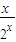 在(0,+∞)单调递增.
在(0,+∞)单调递增.
所以 (n∈N*)是递增数列.(10分)
(n∈N*)是递增数列.(10分)
同理设g(x)= (x>0),
(x>0),
因为g′(x)= •
• =-
=-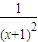 <0(x>0),
<0(x>0),
故g(x)= 在(0,+∞)单调递减.
在(0,+∞)单调递减.
所以Tn= (n∈N*)是递减数列.(12分)
(n∈N*)是递减数列.(12分)
容易计算S1=f(1)= ,S2=f(2)=1,S3=f(3)=1
,S2=f(2)=1,S3=f(3)=1 ,S4=f(4)=1
,S4=f(4)=1 ,
,
T1=g(1)=1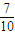 ,T2=g(2)=1
,T2=g(2)=1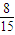 ,T3=g(3)=1
,T3=g(3)=1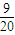 ,T4=g(4)=1
,T4=g(4)=1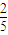 ,
,
显然S1<T1,S2<T2,S3<T3,S4>T4,
所以当n≤3时,Sn<Tn;当n>3时,Sn>Tn.(14分)
点评:本题是对等差数列和等比数列的综合考查.并考查了数列求和的错位相减法.以及数列与函数的综合.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.
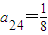 和
和 求出a44,再利用每行上的数从左到右都成等比数列,并且所有公比都等于q来求公比即可.
求出a44,再利用每行上的数从左到右都成等比数列,并且所有公比都等于q来求公比即可.(Ⅱ)先求出ai4,然后在利用第i行成等比数列,且公比
 ,即可求出aij的计算公式;
,即可求出aij的计算公式;(Ⅲ)有(Ⅱ)的结论求出bn的通项,再利用错位相减法求出Sn,然后研究出Sn与Tn=
 对应的函数的单调性,利用单调性来比较Sn与Tn=
对应的函数的单调性,利用单调性来比较Sn与Tn= 的大小即可.
的大小即可.解答:解:(Ⅰ)设第4列公差为d,则
 .
.故
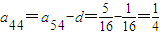 ,于是
,于是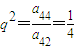 .
.由于aij>0,所以q>0,故
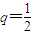 .(3分)
.(3分)(Ⅱ)在第4列中,
 .
.由于第i行成等比数列,且公比
 ,
,所以,
 .(6分)
.(6分)(Ⅲ)由(Ⅱ)可知
 .即bn=
.即bn= .
.所以Sn=b1+b2+b3++bn=a11+a22+a33++ann.
即
 ,
,故
 .
.两式相减,得
 =
= ,
,所以
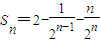 .(8分)
.(8分)设f(x)=2-
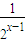 -
- (x>0),
(x>0),即f(x)=2-
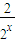 -
-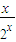 =2-
=2- =2-(2+x)2-x.
=2-(2+x)2-x.因为f′(x)=-[2-x+(2+x)2-x(-1)ln2]=2-x[(2+x)ln2-1]
=2-x[ln22+x-lne]=2-xln
 ,
,且当x>0时,x+2>2.所以22+x>22=4.
于是
 >
> >1.
>1.所以ln
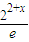 >0.
>0.又2-x>0,
所以在(0,+∞)上f′(x)=2-xln
 >0.
>0.因此函数f(x)=2-
 -
-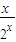 在(0,+∞)单调递增.
在(0,+∞)单调递增.所以
 (n∈N*)是递增数列.(10分)
(n∈N*)是递增数列.(10分)同理设g(x)=
 (x>0),
(x>0),因为g′(x)=
 •
• =-
=-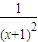 <0(x>0),
<0(x>0),故g(x)=
 在(0,+∞)单调递减.
在(0,+∞)单调递减.所以Tn=
 (n∈N*)是递减数列.(12分)
(n∈N*)是递减数列.(12分)容易计算S1=f(1)=
 ,S2=f(2)=1,S3=f(3)=1
,S2=f(2)=1,S3=f(3)=1 ,S4=f(4)=1
,S4=f(4)=1 ,
,T1=g(1)=1
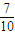 ,T2=g(2)=1
,T2=g(2)=1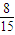 ,T3=g(3)=1
,T3=g(3)=1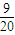 ,T4=g(4)=1
,T4=g(4)=1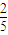 ,
,显然S1<T1,S2<T2,S3<T3,S4>T4,
所以当n≤3时,Sn<Tn;当n>3时,Sn>Tn.(14分)
点评:本题是对等差数列和等比数列的综合考查.并考查了数列求和的错位相减法.以及数列与函数的综合.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.

练习册系列答案
相关题目
在下列由正数排成的数表中,每行上的数从左到右都成等比数列,并且所有公比都等于q,每列上的数从上到下都成等差数列.![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的数,其中
列的数,其中![]() ,
,![]() ,
,![]() .
.
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 求![]() 的计算公式;
的计算公式;
(Ⅲ)设数列{bn}满足bn=ann,{bn}的前![]() 项和为
项和为![]() ,试比较
,试比较![]() 与Tn=
与Tn=![]() ( n∈N*) 的大小,并说明理由.
( n∈N*) 的大小,并说明理由.
在下列由正数排成的数表中,每行上的数从左到右都成等比数列,并且所有公比都等于![]() ,每列上的数从上到下都成等差数列.
,每列上的数从上到下都成等差数列.![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的数,其中
列的数,其中![]() ,
,![]() ,
,![]() .
.
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 求![]() 的计算公式;
的计算公式;
(Ⅲ)设数列{bn}满足bn=ann,{bn}的前![]() 项和为
项和为![]() ,求
,求![]() .
.
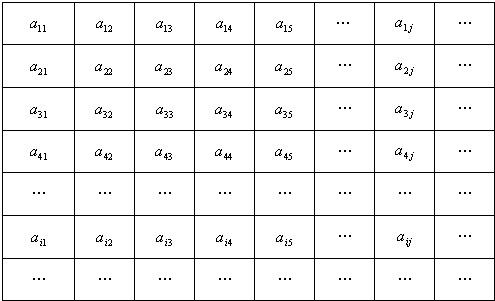
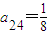 ,a42=1,
,a42=1,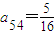 .
.
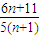 ( n∈N*)的大小,并说明理由.
( n∈N*)的大小,并说明理由.