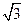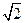题目内容

点M，N分别是曲线ρsinθ=2和ρ=2cosθ-2sinθ上的动点，则|MN|的最小值是（　　）
A．2-
2
B．2+
2
C．3-
2
D．3+
2
由ρsinθ=2，得y=2．
由ρ=2cosθ-2sinθ，得ρ2=2ρcosθ-2ρsinθ，即x2-2x+y2+2y=0．
整理得（x-1）2+（y+1）2=2．
表示以（1，-1）为圆心，以
2
为半径的圆．
∵直线与圆相离，
∴曲线ρsinθ=2和ρ=2cosθ-2sinθ上的动点M，N的距离|MN|的最小值是2-（-1）-
2
=3-
2
．
故选C．
练习册系列答案
相关题目
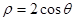（坐标系与参数方程选做题）已知曲线C的极坐标方程为，则曲线C上的点到直线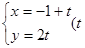为参数）的距离的最小值为           ．

经过点P（2，
π
4
），且垂直于极轴的直线的极坐标方程是______．
若（x，y）与（ρ，θ）（ρ∈R）分别是点M的直角坐标和极坐标，t表示参数，则下列各组曲线：
①θ=
n
6
和sinθ=
1
2
；
②θ=
n
6
和tanθ=
3
3
；
③ρ2-9=0和ρ=3；
④
x=2+
2
2
t
y=3+
1
2
t
和
x=2+
2
t
y=3+
1
2
t
．
其中表示相同曲线的组数为______．
已知曲线C：x2+y2=4，直线L过点P（-1，-2），倾斜角为30°，
（Ⅰ）求直线L的标准参数方程；
（Ⅱ）求曲线C的参数方程．
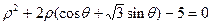
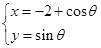点P(x,y)在曲线 (θ为参数,θ∈R)上,则的取值范围是     .
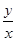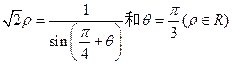已知两直线的极坐标方程分别是,则两直线交点的极坐标为           .
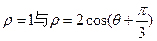若两条曲线的极坐标方程分别为，它们相交于A，B两点，则线段AB的长为（   ）
A．B．C．2D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网