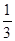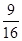题目内容
在区间 内任取两个数
内任取两个数 ,则使方程
,则使方程 的两个根分别作为椭圆与双曲线的离心率的概率为( )
的两个根分别作为椭圆与双曲线的离心率的概率为( )
A. | B. | C. | D. |
C
解析试题分析:依题意,要使方程两根分别作为椭圆,双曲线的离心率,则有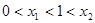 ,令
,令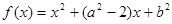 ,所以
,所以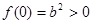 ,
,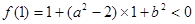 ,所以,
,所以,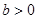 ,
,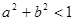 ,故概率为
,故概率为 .选C.
.选C.
考点:1.椭圆、双曲线的性质; 2.几何概型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在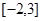 上随机取一个数x,则
上随机取一个数x,则 的概率为( )
的概率为( )
A.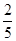 | B. | C.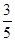 | D.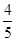 |
在区域D: 内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
内随机取一个点,则此点到点A(1,2)的距离大于2的概率是( )
A. | B. | C. | D. |
若 ,则
,则 的值使得过
的值使得过 可以做两条直线与圆
可以做两条直线与圆
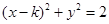 相切的概率等于( )
相切的概率等于( )
A. | B. | C. | D.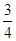 |
在区间[-1,1]上随机取一个数 ,则
,则 的值介于
的值介于 与
与 之间的概率为( )
之间的概率为( )
A. | B. | C. | D. |
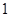 ,
,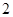 ,
,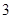 ,
,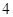 ,
,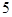 的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )
的五张卡片中任取两张,假设每张卡片被取到的概率相等,且每张卡片上只有一个数字,则取到的两张卡片上的数字之和为偶数的概率为( )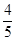
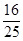
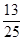
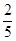
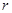 的一个圆,点击圆周上点A后该点在圆周上随机转动,最终落点为B,当线段AB的长不小于
的一个圆,点击圆周上点A后该点在圆周上随机转动,最终落点为B,当线段AB的长不小于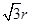 时自动播放音乐,则一次转动能播放出音乐的概率为( )
时自动播放音乐,则一次转动能播放出音乐的概率为( )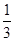
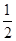
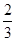
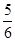
 ,则事件A在一次试验中出现的概率是
,则事件A在一次试验中出现的概率是