题目内容
已知函数![]() 满足2
满足2![]() +
+![]() ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,![]() ,
,![]() 。
。
(1)求函数![]() 解析式;
解析式;
(2)求数列{an}、{bn}的通项公式;
(3)若对任意实数![]() ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时,![]() 恒成立,求k的最小值。
恒成立,求k的最小值。
解:(1)![]() ,∴
,∴![]() ,联立解得
,联立解得![]()
(2)∵![]() ,∴
,∴![]() ,
,
∴![]() 是以1为首项、2为公差的等差数列,
是以1为首项、2为公差的等差数列,
![]() ,∴
,∴![]()
又![]()
![]() ,
,
相加有![]() ,∴
,∴![]()
(3)对任意实数λ∈[0,1]时,![]() 恒成立,
恒成立,
则![]() 恒成立,变形为
恒成立,变形为![]() ,
,![]() 恒成立。
恒成立。
设![]() ,
,
∴ ![]() ,
, ![]()
∴ ![]() ,
, ![]()
∴![]() 或
或![]() ,n∈N+
,n∈N+
故kmin=3

练习册系列答案
相关题目
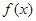 满足对一切
满足对一切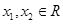 都有
都有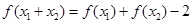 ,且
,且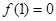 ,当
,当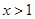 时有
时有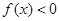 .
.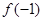 的值;
的值;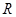 上的单调性;
上的单调性;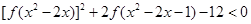 .
.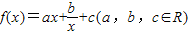 满足f(-1)=0,且对任意x>0都有
满足f(-1)=0,且对任意x>0都有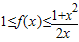 .
.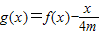 在(0,2]上是减函数,求实数m的取值范围.
在(0,2]上是减函数,求实数m的取值范围.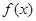 满足:(1)对任意
满足:(1)对任意 ,恒有
,恒有 成立;(2)当
成立;(2)当 时,
时, .若
.若
 ,则满足条件的最小的正实数
,则满足条件的最小的正实数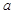 是
是