题目内容
已知函数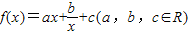 满足f(-1)=0,且对任意x>0都有
满足f(-1)=0,且对任意x>0都有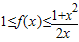 .
.(1)求f(1)的值;
(2)求a,b,c的值;
(3)若
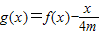 在(0,2]上是减函数,求实数m的取值范围.
在(0,2]上是减函数,求实数m的取值范围.
【答案】分析:(1)对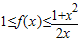 赋值x=1,则可求;
赋值x=1,则可求;
(2)由f(-1)=0,f(1)=1,建立方程组,再借助于对任意x>0都有 ,从而问题得解;
,从而问题得解;
(3)利用单调性的定义,设0<x1<x2≤2可有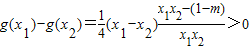 ,从而1-m>x1x2恒成立,而0<x1x2<4,所以1-m≥4,故可求实数m的取值范围.
,从而1-m>x1x2恒成立,而0<x1x2<4,所以1-m≥4,故可求实数m的取值范围.
解答:解:(1)由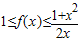 ,令x=1,得1≤f(x)≤1,∴f(1)=1.
,令x=1,得1≤f(x)≤1,∴f(1)=1.
(2)由f(-1)=0,f(1)=1,得 .
.
当x≥0时,
①②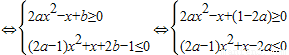
由①式a≤0显然不成立,∴a>0,∵Q(x)=2ax2-x+(1-2a)的图象的对称轴为 ,
,
∴△=1-8a(1-2a)≤0,即(4a-1)2≤0,∴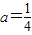 ,
,
从而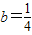 ,而此时②式为(x-1)2≥0,∴
,而此时②式为(x-1)2≥0,∴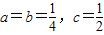 .
.
(3) ,设0<x1<x2≤2,则
,设0<x1<x2≤2,则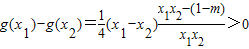 ,∵x1-x2<0,x1x2>0,
,∵x1-x2<0,x1x2>0,
∴x1x2-(1-m)<0,即1-m>x1x2恒成立,而0<x1x2<4,∴1-m≥4,
∴m≤-3.
点评:本题主要考查函数解析式的求解,考查恒成立的处理,采用了赋值法,属于中档题.
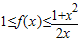 赋值x=1,则可求;
赋值x=1,则可求;(2)由f(-1)=0,f(1)=1,建立方程组,再借助于对任意x>0都有
 ,从而问题得解;
,从而问题得解;(3)利用单调性的定义,设0<x1<x2≤2可有
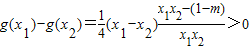 ,从而1-m>x1x2恒成立,而0<x1x2<4,所以1-m≥4,故可求实数m的取值范围.
,从而1-m>x1x2恒成立,而0<x1x2<4,所以1-m≥4,故可求实数m的取值范围.解答:解:(1)由
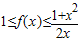 ,令x=1,得1≤f(x)≤1,∴f(1)=1.
,令x=1,得1≤f(x)≤1,∴f(1)=1.(2)由f(-1)=0,f(1)=1,得
 .
.当x≥0时,

①②
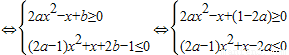
由①式a≤0显然不成立,∴a>0,∵Q(x)=2ax2-x+(1-2a)的图象的对称轴为
 ,
,∴△=1-8a(1-2a)≤0,即(4a-1)2≤0,∴
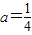 ,
,从而
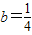 ,而此时②式为(x-1)2≥0,∴
,而此时②式为(x-1)2≥0,∴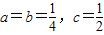 .
.(3)
 ,设0<x1<x2≤2,则
,设0<x1<x2≤2,则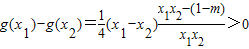 ,∵x1-x2<0,x1x2>0,
,∵x1-x2<0,x1x2>0,∴x1x2-(1-m)<0,即1-m>x1x2恒成立,而0<x1x2<4,∴1-m≥4,
∴m≤-3.
点评:本题主要考查函数解析式的求解,考查恒成立的处理,采用了赋值法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
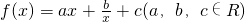 满足f(-1)=0,且对任意x>0都有
满足f(-1)=0,且对任意x>0都有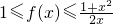 .
.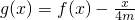 在(0,2]上是减函数,求实数m的取值范围.
在(0,2]上是减函数,求实数m的取值范围. 满足f(2)=1,且方程f(x)=x有且仅有一个实数根.
满足f(2)=1,且方程f(x)=x有且仅有一个实数根. ,对于(Ⅱ)中的数列{an},令
,对于(Ⅱ)中的数列{an},令 ,设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1).
,设Sn为数列{bn}的前n项和,求证:Sn>ln(n+1). 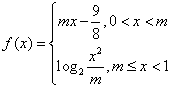 满足f(m2)=-1,则m=( )。
满足f(m2)=-1,则m=( )。