题目内容
选修4-2 矩阵与变换
T是将平面上每个点M(x,y)的横坐标乘2,纵坐标乘4,变到点M(2x,4y).圆C:x2+y2=1在变换T的作用下变成了什么图形?
T是将平面上每个点M(x,y)的横坐标乘2,纵坐标乘4,变到点M(2x,4y).圆C:x2+y2=1在变换T的作用下变成了什么图形?
分析:利用T变换即可得出要求的图形的方程,进而根据圆锥曲线的定义即可得出.
解答:解:设P(x,y)为圆C:x2+y2=1上的任意一点,在变换T的作用下变成了P′(x′,y′),
则x′=2x,y′=4y,于是x=
x′,y=
y′,代入圆C的方程:x2+y2=1得
+
=1,即为所求的方程,是焦点在y轴的椭圆.
则x′=2x,y′=4y,于是x=
| 1 |
| 2 |
| 1 |
| 4 |
| x′2 |
| 4 |
| y′2 |
| 16 |
点评:熟练掌握变换的方法和椭圆的定义是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
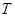 是将平面上每个点
是将平面上每个点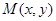 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点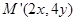 。
。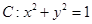 在变换
在变换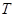 是将平面上每个点
是将平面上每个点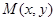 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点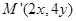 。
。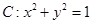 在变换
在变换