题目内容
若方程 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
B
解析试题分析:法一:当a=0时,x=-1,不合题意,故排除C、D.当a=-2时,方程可化为4x2+x+1=0,
而△=1-16<0,无实根,故a=-2不适合,排除A,故选B
法二:f(0)•f(1)<0,即-1×(2a-2)<0,解得a>1,故选B
考点:本试题主要考查了一元二次方程的根的分布与系数的关系,是基础题
点评:解决该试题的关键是能利用特殊值验证法,排除法,得到结论。或者是利用分离参数的思想得到a=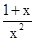 ,结合函数与函数的交点来得到参数a的范围。
,结合函数与函数的交点来得到参数a的范围。

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
函数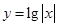 是( )
是( )
A.偶函数,在区间 上单调递增 上单调递增 | B.偶函数,在区间 上单调递减 上单调递减 |
C.奇函数,在区间 上单调递增 上单调递增 | D.奇函数,在区间 上单调递减 上单调递减 |
已知函数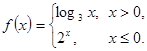 则
则 的值为( )
的值为( )
A.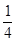 | B.4 | C.2 | D.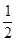 |
设函数 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,则
,则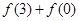 =( )
=( )
| A.3 | B. | C.2 | D. |
三个数 ,
, 之间的大小关系是( )
之间的大小关系是( )
A. ﹤ ﹤ ﹤ ﹤ | B. ﹤ ﹤ ﹤ ﹤  | C. ﹤ ﹤ ﹤ ﹤ | D. ﹤ ﹤ ﹤ ﹤ |
二次函数 中,
中,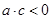 ,则函数的零点个数是( )
,则函数的零点个数是( )
| A.0个 | B.1个 | C.2个 | D.无法确定 |
函数 的单调递增区间是
的单调递增区间是
A. | B. | C.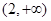 | D. |
在b=loga-2(5-a) 中,实数a的取值范围是( )
| A.a>5,或a<2 | B.2<a<5 | C.2<a<3,或3<a<5 | D.3<a<4 |
 ,则函数
,则函数 的大致图像是( )
的大致图像是( )