题目内容
给出下列三个命题(1)设f(x)是定义在R上的可导函数,f/(x)为函数f(x)的导函数;f/(x0)=0是x0为f(x)极值点的必要不充分条件.
(2)双曲线
| x2 |
| m2+12 |
| y2 |
| 4-m2 |
(3)命题“中国人不都是北京人”的否定是“中国人都是北京人”.
(4)命题“若
| c |
| a |
| d |
| b |
其中正确结论的序号是
分析:由函数极值点与导数的关系,我们易判断(1)的对错;根据双曲线的性质,我们易求出(2)中双曲线中的焦距,进而判断出(2)的真假;根据命题否定的定义,我们易判断(3)的正误;根据不等式的性质,我们可以判断(4)的真假,进而得到结论.
解答:解:(1)∵f(x)是定义在R上的可导函数,
当f/(x0)=0时,x0可能f(x)极值点,也可能不是f(x)极值点,
当x0为f(x)极值点时,f/(x0)=0一定成立,
故f/(x0)=0是x0为f(x)极值点的必要不充分条件,故(1)正确;
双曲线
-
=1中,c2=m2+12+4-m2=16
故c=4,即双曲线的焦距为8与m无关.
故双曲线
-
=1的焦距与m有关为假命题,即(2)错误;
命题“中国人不都是北京人”的否定是“中国人都是北京人”,故(3)正确;
若
-
>0,即
>0,又由bc-ad<0,得到ab<0,故(4)错误.
故答案为:(1),(3)
当f/(x0)=0时,x0可能f(x)极值点,也可能不是f(x)极值点,
当x0为f(x)极值点时,f/(x0)=0一定成立,
故f/(x0)=0是x0为f(x)极值点的必要不充分条件,故(1)正确;
双曲线
| x2 |
| m2+12 |
| y2 |
| 4-m2 |
故c=4,即双曲线的焦距为8与m无关.
故双曲线
| x2 |
| m2+12 |
| y2 |
| 4-m2 |
命题“中国人不都是北京人”的否定是“中国人都是北京人”,故(3)正确;
若
| c |
| a |
| d |
| b |
| bc-ad |
| ab |
故答案为:(1),(3)
点评:本题考查的知识点是命题的真假的判断,利用导函数求函数的极值,双曲线的焦距,不等式的性质等,熟练掌握上述定义和性质是解答本题的关键.

练习册系列答案
相关题目
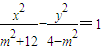 的焦距与m有关
的焦距与m有关 ”
”