题目内容
给出下列三个命题(1)若tanA?tanB>1,则△ABC一定是钝角三角形;
(2)若sin2A+sin2B=sin2C,则△ABC一定是直角三角形;
(3)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC一定是等边三角形.
以上正确命题的个数有( )
A.0个
B.1个
C.2个
D.3个
【答案】分析:通过举反例可得(1)不正确,利用和差化积公式可得△ABC一定是等腰三角形,不能推出△ABC一定是直角三角形,
故(2)不正确.对于(3),由题意可得cos(A-B)=cos(B-C)=cos(C-A)=1,可得A=B=C=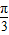 ,故△ABC一定是等边三角形,得到(3)正确.
,故△ABC一定是等边三角形,得到(3)正确.
解答:解:(1)不正确,如等边△ABC中,A=B=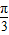 ,尽管满足tanA?tanB>1,但△ABC不是钝角三角形.
,尽管满足tanA?tanB>1,但△ABC不是钝角三角形.
(2)若sin2A+sin2B=sin2C,则有2sin(A+B)cos(A-B)=2sin(A+B),
再由-π<A-B<π 可得,cos(A-B)=1,A-B=0.
故△ABC一定是等腰三角形,不能推出△ABC一定是直角三角形,故(2)不正确.
(3)△ABC中,若cos(A-B)cos(B-C)cos(C-A)=1,
则由-1≤cos(A-B)≤1,-1≤cos(B-C)≤1,-1≤cos(C-A)≤1 可得,
cos(A-B)=cos(B-C)=cos(C-A)=1,
∴A-B=B-C=C-A=0,∴A=B=C= ,
,
故△ABC一定是等边三角形,故(3)正确.
故选A.
点评:本题主要考查三角形的内角和公式,判断三角形的形状的方法,通过举反例来说明某个命题不正确,是一种简单有效
的方法,属于中档题.
故(2)不正确.对于(3),由题意可得cos(A-B)=cos(B-C)=cos(C-A)=1,可得A=B=C=
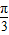 ,故△ABC一定是等边三角形,得到(3)正确.
,故△ABC一定是等边三角形,得到(3)正确.解答:解:(1)不正确,如等边△ABC中,A=B=
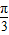 ,尽管满足tanA?tanB>1,但△ABC不是钝角三角形.
,尽管满足tanA?tanB>1,但△ABC不是钝角三角形.(2)若sin2A+sin2B=sin2C,则有2sin(A+B)cos(A-B)=2sin(A+B),
再由-π<A-B<π 可得,cos(A-B)=1,A-B=0.
故△ABC一定是等腰三角形,不能推出△ABC一定是直角三角形,故(2)不正确.
(3)△ABC中,若cos(A-B)cos(B-C)cos(C-A)=1,
则由-1≤cos(A-B)≤1,-1≤cos(B-C)≤1,-1≤cos(C-A)≤1 可得,
cos(A-B)=cos(B-C)=cos(C-A)=1,
∴A-B=B-C=C-A=0,∴A=B=C=
 ,
,故△ABC一定是等边三角形,故(3)正确.
故选A.
点评:本题主要考查三角形的内角和公式,判断三角形的形状的方法,通过举反例来说明某个命题不正确,是一种简单有效
的方法,属于中档题.

练习册系列答案
相关题目
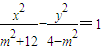 的焦距与m有关
的焦距与m有关 ”
”