题目内容
在△ABC中,若sin2A+sin2B<sin2C,则△ABC的形状是( )
| A.钝角三角形 | B.直角三角形 |
| C.锐角三角形 | D.不能确定 |
A
【思路点拨】利用正弦定理转化为边的关系,而后利用余弦定理判断.
解:由sin2A+sin2B<sin2C得
a2+b2<c2,即a2+b2-c2<0.
又∵cosC=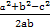 ,故cosC<0.
,故cosC<0.
又∵0<C<π,故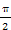 <C<π,
<C<π,
所以△ABC是钝角三角形.
【方法技巧】三角形形状判断技巧
三角形形状的判断问题是解三角形部分的一个重要题型,也是高考的热点问题,因而正确快速地判断是解题的关键.其基本技巧就是利用正、余弦定理快速实现边角互化,常规是边化角,再利用三角恒等变换公式结合三角形中角的关系正确判断三角形的形状.
解:由sin2A+sin2B<sin2C得
a2+b2<c2,即a2+b2-c2<0.
又∵cosC=
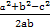 ,故cosC<0.
,故cosC<0.又∵0<C<π,故
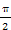 <C<π,
<C<π,所以△ABC是钝角三角形.
【方法技巧】三角形形状判断技巧
三角形形状的判断问题是解三角形部分的一个重要题型,也是高考的热点问题,因而正确快速地判断是解题的关键.其基本技巧就是利用正、余弦定理快速实现边角互化,常规是边化角,再利用三角恒等变换公式结合三角形中角的关系正确判断三角形的形状.

练习册系列答案
相关题目
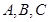 所对的边长分别为
所对的边长分别为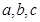 ,
,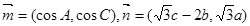 ,且
,且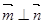 .
.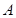 的大小;
的大小;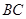 边上的中线
边上的中线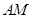 的长为
的长为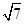 ,求
,求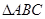 的面积.
的面积.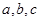 满足
满足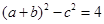 ,且
,且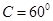 ,则
,则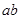 的值为( )
的值为( )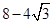 C.
C.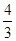 D.
D.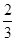
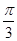 ,且△ABC的面积为
,且△ABC的面积为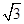 ,求a、b的值;
,求a、b的值;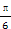 ,S△ABC=
,S△ABC= ,则b= .
,则b= .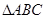 的内角
的内角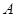 、
、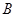 、
、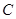 所对的边分别是
所对的边分别是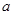 ,
,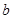 ,
,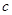 .若
.若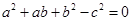 ,则角
,则角
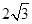
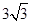
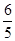 bc,则sin(B+C)=( )
bc,则sin(B+C)=( )