题目内容
有下列说法中,其中正确的个数是( )
①f(x)=2lgx与g(x)=lgx2表示同一函数;
②函数y=ax-1(0<a<1)的图象一定过点(1,1);
③若tanθ=
,则sinθcosθ=
.
①f(x)=2lgx与g(x)=lgx2表示同一函数;
②函数y=ax-1(0<a<1)的图象一定过点(1,1);
③若tanθ=
| 1 |
| 3 |
| 3 |
| 10 |
分析:①要判断两个函数是否是同一个函数,需要从三个方面来分析,即定义域,对应法则和值域,
②在函数y=ax-1中,当x=1时,y=a0=1,由此能得到正确答案.
③利用三角函数的同角公式得sinθcosθ=
,再分子分母同除以cos2θ化成关于tanθ的表达式即可求得结果.
②在函数y=ax-1中,当x=1时,y=a0=1,由此能得到正确答案.
③利用三角函数的同角公式得sinθcosθ=
| sinθcosθ |
| sin2θ+cos2θ |
解答:解:①要判断两个函数是否是同一个函数,需要从三个方面来分析,
即定义域,对应法则和值域,
对于①选项,f(x)的定义域为R+,g(x)的定义域为{x|x≠0},∴不是同一函数.
②在函数y=ax-1中,
当x=1时,y=a0=1,
∴函数y=ax-1的图象一定经过点(1,1).正确;
③sinθcosθ=
=
=
=
,正确.
故选B.
即定义域,对应法则和值域,
对于①选项,f(x)的定义域为R+,g(x)的定义域为{x|x≠0},∴不是同一函数.
②在函数y=ax-1中,
当x=1时,y=a0=1,
∴函数y=ax-1的图象一定经过点(1,1).正确;
③sinθcosθ=
| sinθcosθ |
| sin2θ+cos2θ |
| tanθ |
| tan2θ+1 |
| ||
(
|
| 3 |
| 10 |
故选B.
点评:本题考查命题的真假判断与应用、指数函数的性质和应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 如图是根据人体的脂肪含量和年龄关系的调查数据所绘制的散点图.有下列说法,其中所有正确的序号是
如图是根据人体的脂肪含量和年龄关系的调查数据所绘制的散点图.有下列说法,其中所有正确的序号是 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点;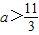 ;
; 与g(x)=x的图象没有公共点;
与g(x)=x的图象没有公共点; ;
;