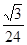题目内容
一正三棱锥A—BCD,其底面边长为a,侧棱长为2a,过点B作与侧棱AC、AD相交的截面,在这样的截面三角形中.(1)求周长的最小值;(2)求最小周长时的截面面积.
解析:如图甲所示,设截面与AC、AD的交点分别为M、N,将侧棱AB剪开后,将侧面展开铺平,当B′、M′、N′、B在一条直线上时,截面周长最短(如图乙).
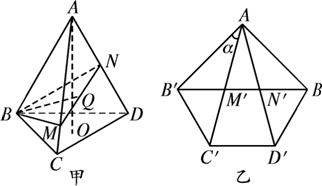
(1)在△B′C′M′和△A′M′N′中,∠B′M′C′=∠A′M′N′,由展开图可知∠A′M′N′=∠A′N′M′,
∴∠A′M′N′=∠A′C′D′=∠A′C′B′.
故有∠B′M′C′=∠M′C′B′,
∴B′M′=B′C′=a,同理N′B=a,
由△A′C′D′—△B′C′M′,
∴C′M′=![]() ,∴A′M′=
,∴A′M′=![]() ,
,
∴![]() ,即
,即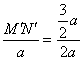 ,
,
∴M′N′=![]() ,故B′B=
,故B′B=![]() ,即周长的最小值为
,即周长的最小值为![]() .
.
(2)由展开的图可知周长最小时的截面△BMN为等腰三角形,且BM=BN=a,MN=3a[]4,∴MN上的高
![]() ,
,
∴S△BMN=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
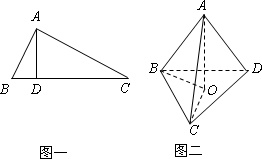
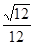 B.
B.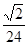 C.
C.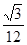 D.
D.