题目内容
(本小题满分14分)
设函数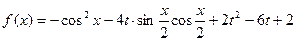 (
( ).
).
(1)当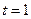 时,求
时,求 的最小值;
的最小值;
(2)若 ,将
,将 的最小值记为
的最小值记为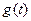 ,求
,求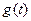 的表达式;
的表达式;
(3)当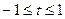 时,关于
时,关于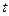 的方程
的方程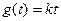 有且仅有一个实根,求实数
有且仅有一个实根,求实数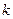 的取值范围.
的取值范围.
设函数
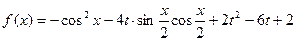 (
( ).
).(1)当
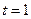 时,求
时,求 的最小值;
的最小值;(2)若
 ,将
,将 的最小值记为
的最小值记为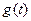 ,求
,求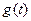 的表达式;
的表达式;(3)当
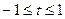 时,关于
时,关于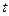 的方程
的方程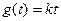 有且仅有一个实根,求实数
有且仅有一个实根,求实数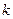 的取值范围.
的取值范围.(1)由已知有: 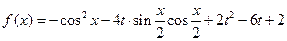
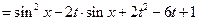
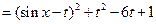 ,……………………………2分
,……………………………2分
∵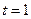
∴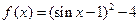
∴当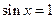 时,
时,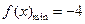 ………………………………………………4分
………………………………………………4分
(2)由于 ,∴
,∴ 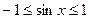 ,
,
∴ 当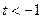 时,则
时,则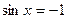 时,
时,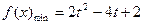 ;
;
当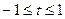 时,则
时,则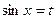 时,
时,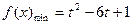 ;
;
当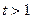 时,则当
时,则当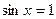 时,
时,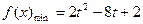 ;
;
综上,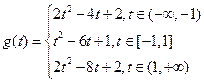 . ……………………………8分
. ……………………………8分
(3)当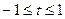 时,
时,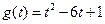 ,
,
方程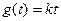 即
即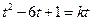 ,
,
即方程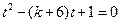 在区间
在区间 有且仅有一个实根,……………………………9分
有且仅有一个实根,……………………………9分
令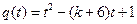 ,则有:
,则有:
解法一、①若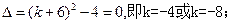
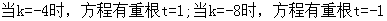
∴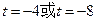 ………………………………………………………………10分
………………………………………………………………10分
②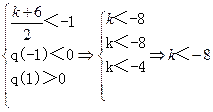 或
或 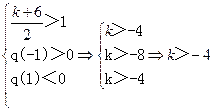
综上所述,当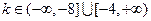 时,方程
时,方程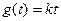 在区间
在区间 有且仅有一个实根.……14分
有且仅有一个实根.……14分
解法二、由零点存在定理得
①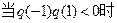 ,
, 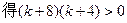 ,
,
∴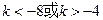 ; …………………………………………………………………10分
; …………………………………………………………………10分
②当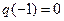 时,
时,
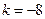 ,此时
,此时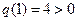 ,符合题意;
,符合题意;
③当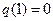 时,
时, 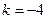 ,此时
,此时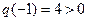 ,符合题意;
,符合题意;
综上,当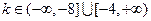 时,方程
时,方程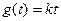 在区间
在区间 有且仅有一个实根.……14分
有且仅有一个实根.……14分
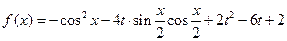
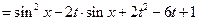
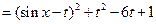 ,……………………………2分
,……………………………2分∵
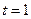
∴
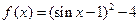
∴当
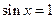 时,
时,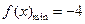 ………………………………………………4分
………………………………………………4分(2)由于
 ,∴
,∴ 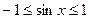 ,
,∴ 当
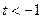 时,则
时,则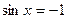 时,
时,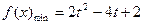 ;
;当
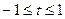 时,则
时,则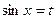 时,
时,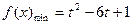 ;
;当
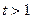 时,则当
时,则当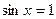 时,
时,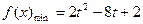 ;
;综上,
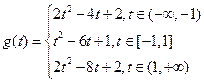 . ……………………………8分
. ……………………………8分(3)当
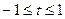 时,
时,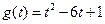 ,
,方程
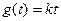 即
即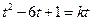 ,
, 即方程
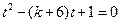 在区间
在区间 有且仅有一个实根,……………………………9分
有且仅有一个实根,……………………………9分令
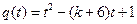 ,则有:
,则有:解法一、①若
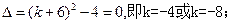
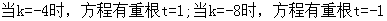
∴
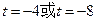 ………………………………………………………………10分
………………………………………………………………10分②
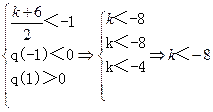 或
或 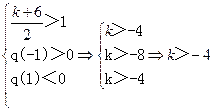
综上所述,当
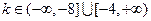 时,方程
时,方程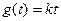 在区间
在区间 有且仅有一个实根.……14分
有且仅有一个实根.……14分解法二、由零点存在定理得
①
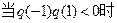 ,
, 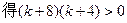 ,
,∴
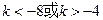 ; …………………………………………………………………10分
; …………………………………………………………………10分②当
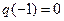 时,
时,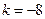 ,此时
,此时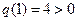 ,符合题意;
,符合题意;③当
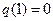 时,
时, 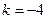 ,此时
,此时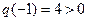 ,符合题意;
,符合题意;综上,当
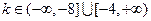 时,方程
时,方程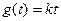 在区间
在区间 有且仅有一个实根.……14分
有且仅有一个实根.……14分略

练习册系列答案
相关题目
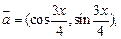
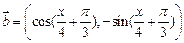
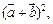 求f(x)解析式及单调递增区间.
求f(x)解析式及单调递增区间.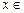
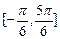 ,求函数f(x)的最大值和最小值.
,求函数f(x)的最大值和最小值. 是偶函数.
是偶函数. ;
; 的图像先纵坐标不变,横坐标缩短为原来的
的图像先纵坐标不变,横坐标缩短为原来的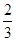 倍,再向左平移
倍,再向左平移 个单位,然后向上平移1个单位得到
个单位,然后向上平移1个单位得到 的图像,若关于
的图像,若关于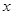 的方程
的方程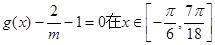 有且只有两个不同的根,求
有且只有两个不同的根,求 的范围.
的范围.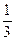 ,则A=____________.(用反三角函数表示)w
,则A=____________.(用反三角函数表示)w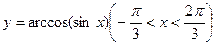 的值域是( )
的值域是( ) 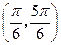
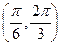
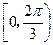

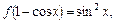 则
则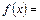 ___________(不必标明定义域)
___________(不必标明定义域) 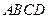 ,
,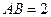 ,
,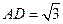 ,
,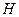 是
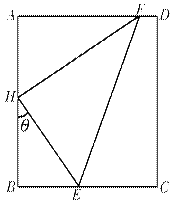
是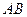 的中点,在该花园中有一花圃其形状是以
的中点,在该花园中有一花圃其形状是以 ,其中E、F分别落在线段
,其中E、F分别落在线段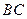 和线段
和线段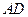 上如图.分别记
上如图.分别记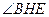 为
为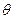 (
(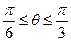 ),
),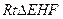 的周长为
的周长为 ,
,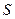 。
。
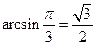
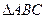 中,a = 6,b=4,C=
中,a = 6,b=4,C=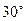 ,则
,则