题目内容
将红、黑、蓝、黄 个不同的小球放入
个不同的小球放入 个不同的盒子,每个盒子至少放一个球,且红球和蓝球不能放在同一个盒子,则不同的放法的种数为( )
个不同的盒子,每个盒子至少放一个球,且红球和蓝球不能放在同一个盒子,则不同的放法的种数为( )
A. | B. | C. | D. |
C
解析试题分析:将4个小球放入3个不同的盒子,
先在4个小球中任取2个作为1组,再将其与其他2个小球对应3个盒子,共有C42A33=36种情况,
若红球和蓝球放到同一个盒子,则黑、黄球放进其余的盒子里,有A33=6种情况,
则红球和蓝球不放到同一个盒子的放法种数为36-6=30种;
故选C.
考点:简单组合应用问题。
点评:简单题,注意应用间接法,可以避免分类讨论,且简化计算过程。

练习册系列答案
相关题目
从5双不同的手套中任取4只,恰有两只是同一双的概率为( )
A.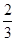 | B.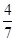 | C.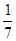 | D.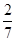 |
从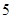 位男数学教师和
位男数学教师和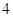 位女数学教师中选出
位女数学教师中选出 位教师派到
位教师派到 个班担任班主任(每班
个班担任班主任(每班 位班主任),要求这
位班主任),要求这 位班主任中男女教师都有,则不同的选派方案共有( )
位班主任中男女教师都有,则不同的选派方案共有( )
| A.210 | B.420 | C.630 | D.840 |
从6人中选4人分别到北京、哈尔滨、广州、成都四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且在这6人中甲、乙不去哈尔滨游览,则不同的选择方案共有
| A.300种 | B.240种 | C.144种 | D.96种 |
在 展开式中,
展开式中, 的系数为( ).
的系数为( ).
| A.360 | B.180 | C.﹣360 | D.-180 |
若 的展开式中各项系数和为
的展开式中各项系数和为 ,则展开式中系数最大的项为( )
,则展开式中系数最大的项为( )
| A.第3项 | B.第4项 | C.第5项 | D.第6项 |
数学中无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“回文数”,如: 88,454,7337,43534等都是回文数,体现对称美,读起来还真有趣!那么六位的回文数共有( )个.
| A.800 | B.810 | C.900 | D.1000 |
2013年第12届全国运动会举行期间,某校4名大学生申请当A,B,C三个比赛项目的志愿者,组委会接受了他们的申请,每个比赛项目至少分配一人,每人只能服务一个比赛项目,若甲要求不去服务A比赛项目,则不同的安排方案共有( )
| A.20种 | B.24种 | C.30种 | D.36种 |
设函数 , 则当x>0时,
, 则当x>0时,  表达式的展开式中常数项为 ( )
表达式的展开式中常数项为 ( )
| A.-20 | B.20 | C.-15 | D.15 |