题目内容
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 (n∈N*).
(n∈N*).(Ⅰ)证明数列{xn}是等比数列;
(Ⅱ)把数列{xn}中所有项按如图所示的规律排成一个三角形数表,当x3=8,x7=128时,求第m行各数的和;
(Ⅲ)对于(Ⅱ)中的数列{xn},证明:
 .
.
【答案】分析:(Ⅰ)由题设条件知anlgxn=an+1lgxn+1=an+2lgxn+2.设anlgxn=an+1lgxn+1=an+2lgxn+2=p,有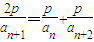 ,由此导出xn+12=xnxn+2,所以数列{xn}是等比数列.
,由此导出xn+12=xnxn+2,所以数列{xn}是等比数列.
(Ⅱ)由题意知{xn}的公比为q=2.xn=x3qn-3=8×2n-3=2n.由此能够推导出第m行各数的和为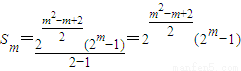 .
.
(Ⅲ)由xn=2n,知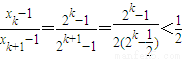 .所以
.所以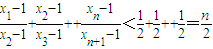 .
.
由此入手能够导出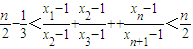 .
.
解答:解:(Ⅰ)证明:因为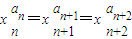 ,且数列{xn}中各项都是正数,
,且数列{xn}中各项都是正数,
所以anlgxn=an+1lgxn+1=an+2lgxn+2.
设anlgxn=an+1lgxn+1=an+2lgxn+2=p,①
因为数列{an}是调和数列,故an≠0,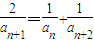 .
.
所以,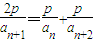 .②
.②
由①得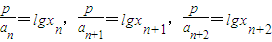 ,代入②式得,
,代入②式得,
所以2lgxn+1=lgxn+lgxn+2,即lgxn+12=lg(xnxn+2).
故xn+12=xnxn+2,所以数列{xn}是等比数列.(5分)
(Ⅱ)设{xn}的公比为q,则x3q4=x7,即8q4=128.由于xn>0,故q=2.
于是xn=x3qn-3=8×2n-3=2n.
注意到第n(n=1,2,3,)行共有n个数,
所以三角形数表中第1行至第m-1行共含有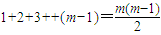 个数.
个数.
因此第m行第1个数是数列{xn}中的第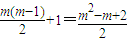 项.
项.
故第m行第1个数是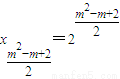 ,
,
所以第m行各数的和为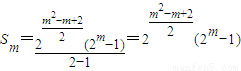 .(9分)
.(9分)
(Ⅲ)因为xn=2n,所以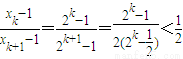 .
.
所以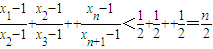 .
.
又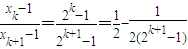 =
=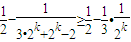 (k=1,2,3,,n),
(k=1,2,3,,n),
所以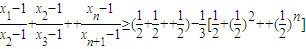
= .
.
所以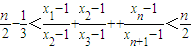 .(14分)
.(14分)
点评:本题考查数列知识的综合运用,难度较大,解题时要注意挖掘隐含条件,灵活运用公式.
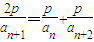 ,由此导出xn+12=xnxn+2,所以数列{xn}是等比数列.
,由此导出xn+12=xnxn+2,所以数列{xn}是等比数列.(Ⅱ)由题意知{xn}的公比为q=2.xn=x3qn-3=8×2n-3=2n.由此能够推导出第m行各数的和为
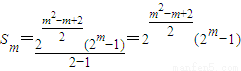 .
.(Ⅲ)由xn=2n,知
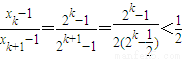 .所以
.所以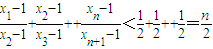 .
.由此入手能够导出
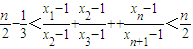 .
.解答:解:(Ⅰ)证明:因为
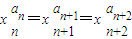 ,且数列{xn}中各项都是正数,
,且数列{xn}中各项都是正数,所以anlgxn=an+1lgxn+1=an+2lgxn+2.
设anlgxn=an+1lgxn+1=an+2lgxn+2=p,①
因为数列{an}是调和数列,故an≠0,
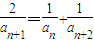 .
.所以,
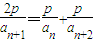 .②
.②由①得
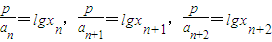 ,代入②式得,
,代入②式得,所以2lgxn+1=lgxn+lgxn+2,即lgxn+12=lg(xnxn+2).
故xn+12=xnxn+2,所以数列{xn}是等比数列.(5分)
(Ⅱ)设{xn}的公比为q,则x3q4=x7,即8q4=128.由于xn>0,故q=2.
于是xn=x3qn-3=8×2n-3=2n.
注意到第n(n=1,2,3,)行共有n个数,
所以三角形数表中第1行至第m-1行共含有
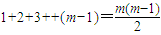 个数.
个数.因此第m行第1个数是数列{xn}中的第
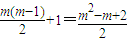 项.
项.故第m行第1个数是
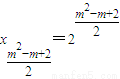 ,
,所以第m行各数的和为
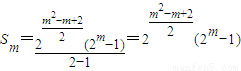 .(9分)
.(9分)(Ⅲ)因为xn=2n,所以
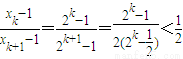 .
.所以
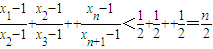 .
.又
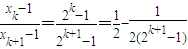 =
=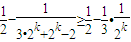 (k=1,2,3,,n),
(k=1,2,3,,n),所以
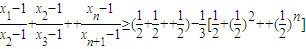
=
 .
.所以
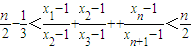 .(14分)
.(14分)点评:本题考查数列知识的综合运用,难度较大,解题时要注意挖掘隐含条件,灵活运用公式.

练习册系列答案
相关题目
 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
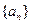 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列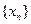 ,满足
,满足
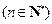 .
.
 时,求第
时,求第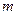 行各数的和;
行各数的和;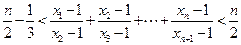 .
.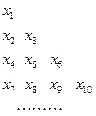
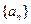 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列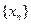 ,满足
,满足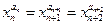
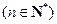 .
.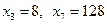 时,求第
时,求第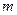 行各数的和;
行各数的和;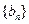 满足
满足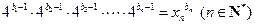 ,求证:数列
,求证:数列 是调和数列,对于各项都是正数的数列
是调和数列,对于各项都是正数的数列 ,满足
,满足
 .
. (Ⅰ)求证:数列
(Ⅰ)求证:数列 时,求第
时,求第 行各数的和;
行各数的和; 满足
满足 ,求证:数列
,求证:数列