题目内容

(1)求数列
 的通项公式;
的通项公式; (2)求数列
 的前n项和
的前n项和 ;
;(3)令
 ,求数列
,求数列 的前n项和
的前n项和 。
。解:(1)因为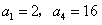 ,所以
,所以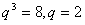 ,
,
所以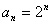 。
。
(2)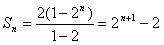 ;
;
(3)因为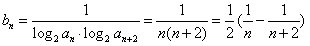 ,
,
所以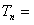
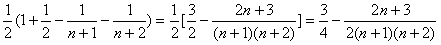 。
。
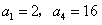 ,所以
,所以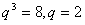 ,
, 所以
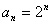 。
。(2)
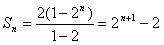 ;
;(3)因为
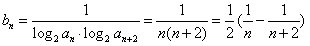 ,
,所以
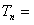
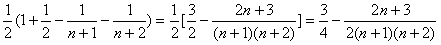 。
。
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
题目内容

 的通项公式;
的通项公式;  的前n项和
的前n项和 ;
; ,求数列
,求数列 的前n项和
的前n项和 。
。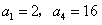 ,所以
,所以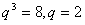 ,
, 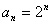 。
。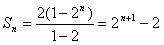 ;
;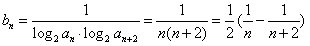 ,
,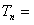
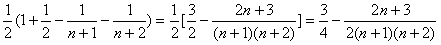 。
。
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案