题目内容
(08年静安区质检文)我们用部分自然数构造如下的数表:用![]() 表示第
表示第![]() 行第
行第![]() 个数(
个数(![]() 为正整数),使
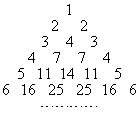
为正整数),使![]() ;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第
;每行中的其余各数分别等于其“肩膀”上的两个数之和(第一、二行除外,如图),设第![]() (
(![]() 为正整数)行中各数之和为
为正整数)行中各数之和为![]() .
.
(1)试写出![]() ,并推测
,并推测![]() 和
和![]() 的关系(无需证明);
的关系(无需证明);
(2)证明数列![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式
的通项公式![]() ;
;
(3)数列![]() 中是否存在不同的三项
中是否存在不同的三项![]() (
(![]() 为正整数)恰好成等差数列?若存在,求出
为正整数)恰好成等差数列?若存在,求出![]() 的关系;若不存在,请说明理由.
的关系;若不存在,请说明理由.
解析:(1)![]() ;
;![]() (或
(或![]() );
);
事实上,![]()
![]()
![]()
![]()
即![]() ;
;
(2)由(1) ![]() ,
,
所以![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,即
,即![]()
(注:若考虑![]() ,且不讨论
,且不讨论![]() ,扣1分)
,扣1分)
(3)若数列![]() 中存在不同的三项
中存在不同的三项![]() 恰好成等差数列,不妨设
恰好成等差数列,不妨设![]() ,
,
显然,![]() 是递增数列,则
是递增数列,则![]()
即![]() ,于是
,于是![]()
由![]() 且
且![]() 知,
知,![]() ,
,
∴等式的左边为偶数,右边为奇数,不成立,故数列![]() 中不存在不同的三项
中不存在不同的三项![]() 恰好成等差数列.
恰好成等差数列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目