题目内容
已知函数f(x)=|log2|x﹣1||,且关于x的方程[f(x)]2+af(x)+2b=0有6个不同的实数解,若最小的实数解为﹣1,则a+b的值为
| A.-2 | B.-1 | C.0 | D.1 |
B
试题分析:根据题意,由于函数f(x)=|log2|x﹣1||,且关于x的方程[f(x)]2+af(x)+2b=0有6个不同的实数解,解:作出函数f(x)=|log2|x-1||的图象,
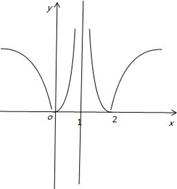
∵方程[f(x)]2+af(x)+2b=0有6个不同的实数解,∴如图所示:令t=f(x),方程[f(x)]2+af(x)+2b=0转化为:t2+at+2b=0则方程有一零根和一正根,又∵最小的实数解为-3∴f(-3)=1,∴方程:t2+at+2b=0的两根是0和2,由韦达定理得:a=-2,b=0,∴a+b=-2,故选B
点评:解决的关键是对于函数与方程的等价转化思想的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为 .
.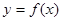 的解析式;
的解析式;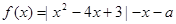 恰有三个不同的零点,则实数a的值是( )
恰有三个不同的零点,则实数a的值是( )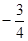
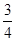
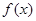 的定义域为开区间
的定义域为开区间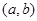 ,导函数
,导函数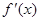 在
在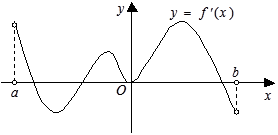
 是函数
是函数 图像上的点,
图像上的点, 是函数
是函数 图像上的点,且
图像上的点,且 两点之间的距离
两点之间的距离 能取到最小值
能取到最小值 ,那么将
,那么将 和
和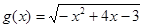 之间的距离是 .
之间的距离是 .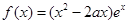 的图象大致是
的图象大致是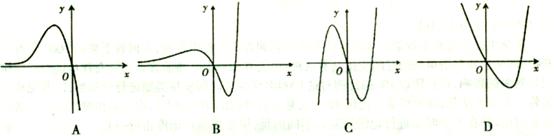
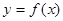 的图像是中心在原点,焦点在
的图像是中心在原点,焦点在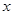 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式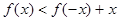 的解集为 ( )
的解集为 ( )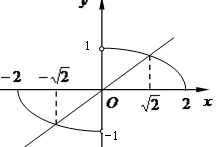
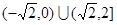
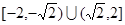

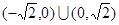
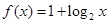 与
与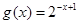 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )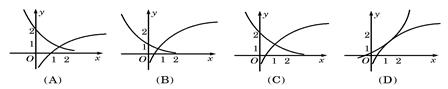
 是函数
是函数 的零点,若有
的零点,若有 ,则
,则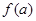 的值满足
的值满足

