题目内容
已知函数 ,函数
,函数 ,若存在
,若存在 ,使得
,使得 成立,则实数
成立,则实数 的取值范围是 。
的取值范围是 。
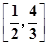
解析试题分析:当x∈[0,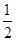 ]时,f(x)=
]时,f(x)=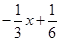 ∈[0,
∈[0,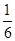 ],当x∈
],当x∈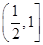 时,f(x)=
时,f(x)=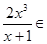 (
(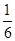 ,1],故x∈[0,1]时,f(x)的值域为[0,1],
,1],故x∈[0,1]时,f(x)的值域为[0,1], 值域是[2-2a,2-
值域是[2-2a,2-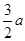 ],∵存在
],∵存在 ,使得
,使得 成立,∴[0,1]∩[2-2a,2-
成立,∴[0,1]∩[2-2a,2-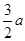 ]≠∅,若[0,1]∩[2-2a,2-
]≠∅,若[0,1]∩[2-2a,2-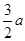 ]=∅,则2-2a>1或2-
]=∅,则2-2a>1或2-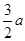 <0,即a<
<0,即a<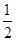 或a>
或a>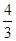 ,
,
∴a的取值范围是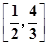
考点:本题考查了函数与方程
点评:解题的关键是通过看两函数值域之间的关系来确定a的范围

练习册系列答案
相关题目
 若
若 ,则实数
,则实数 的取值范围是 .
的取值范围是 . 的定义域为 。
的定义域为 。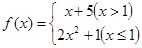 ,则
,则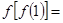 .
.  的定义域为
的定义域为 ,则函数
,则函数 的定义域为 .
的定义域为 .  的定义域为A,若
的定义域为A,若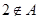 ,则
,则 的取值范围为 .
的取值范围为 . ,其中
,其中 ,若动直线
,若动直线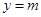 与函数
与函数 的图像有三个不同的交点,则实数
的图像有三个不同的交点,则实数 的取值范围是______________.
的取值范围是______________.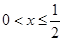 时,
时, ,则
,则 的取值范围 .
的取值范围 .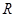 上的偶函数
上的偶函数 在区间
在区间 上是单调递增,若
上是单调递增,若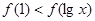 ,则
,则 的取值范围是
的取值范围是