题目内容
设圆锥曲线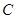 的两个焦点分别为
的两个焦点分别为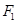 、
、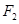 ,若曲线
,若曲线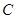 上存在点
上存在点 满足
满足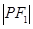 :
: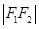 :
: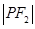 =4:3:2,则曲线
=4:3:2,则曲线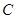 的离心率等于(
)
的离心率等于(
)
A.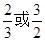 B.
B.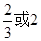 C.
C.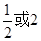 D.
D.
【答案】
D
【解析】
试题分析:根据题意,该圆锥曲线可能是椭圆,也可能是双曲线,那么当为前者时,则有点 满足
满足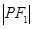 :
: :
: =4:3:2,由椭圆定义可知,2a=6,2c=3则离心率为
=4:3:2,由椭圆定义可知,2a=6,2c=3则离心率为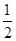 ,当当为后者时,则有点
,当当为后者时,则有点 满足
满足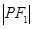 :
: :
: =4:3:2,由双曲线定义可知,2a=2,2c=3则离心率为
=4:3:2,由双曲线定义可知,2a=2,2c=3则离心率为 ,故可知结论为
,故可知结论为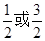 ,选D
,选D
考点:圆锥曲线的性质
点评:主要是考查了圆锥曲线的共同的性质的运用,属于基础题。

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 的两个焦点分别为
的两个焦点分别为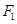 、
、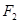 ,若曲线
,若曲线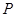 满足
满足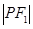 :
: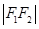 :
: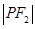 =4:3:2,则曲线
=4:3:2,则曲线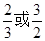 B.
B.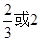 C.
C.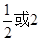 D.
D.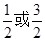
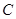 的两个焦点分别为
的两个焦点分别为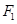 、
、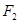 ,若曲线
,若曲线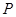 满足
满足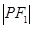 :
: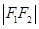 :
: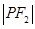 =4:3:2,则曲线
=4:3:2,则曲线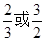 B.
B.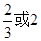 C.
C. D.
D.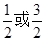
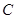 的两个焦点分别为
的两个焦点分别为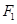 、
、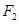 ,若曲线
,若曲线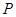 满足
满足 :
: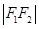 :
: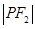 =4:3:2,则曲线
=4:3:2,则曲线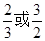 B.
B.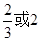 C.
C.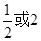 D.
D.
 的两个焦点分别为
的两个焦点分别为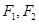 ,若曲线
,若曲线 满足
满足 ,则曲线
,则曲线 B.
B. 或2 C.
或2 C. 2
D.
2
D.