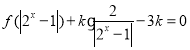题目内容
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元,求:
(1)仓库顶部面积![]() 的最大允许值是多少?
的最大允许值是多少?
(2)为使![]() 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
【答案】(1)100;(2)15米
【解析】
本试题主要是考查了函数模型在实际生活中的运用。
(1)设铁栅长为x米,一堵砖墙长为y米,则S=xy,
由题意得40x+2×45y+20xy="3" 200,然后运用不等式求解得到最值。
(2)当![]() 即x=15米,可知结论。
即x=15米,可知结论。
(1)设铁栅长为x米,一堵砖墙长为y米,则S=xy,
由题意得40x+2×45y+20xy="3" 200,
应用二元均值不等式,得3 200≥2![]() +20xy,即S+6
+20xy,即S+6![]() ≤160,
≤160,
而(![]() +16)(
+16)(![]() -10)≤0.
-10)≤0.
∴![]() ≤10
≤10![]() S≤100.
S≤100.
因此S的最大允许值是100米2.
(2)当![]() 即x=15米,
即x=15米,
即铁栅的长为15米.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中恰有1名男生的概率是多少?
(3)是否有![]() 把握认为学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
把握认为学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.
附:参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
![]() ,其中
,其中![]()