题目内容
已知函数f（x）是可导函数，且满足
，则在曲线y=f（x）上的点A（1，f（1））的切线斜率是（ ）A．-1
B．2
C．1
D．-2
【答案】分析：函数f（x）是可导函数，且满足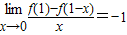
，可得
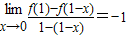，利用导数的定义，即可求得切线斜率．
解答：解：∵函数f（x）是可导函数，且满足
，
∴
∴f′（1）=-1
∴在曲线y=f（x）上的点A（1，f（1））的切线斜率是-1
故选A．
点评：本题考查导数的概念与导数的几何意义，解题的关键是正确理解导数的概念．
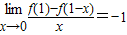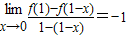，可得，利用导数的定义，即可求得切线斜率．解答：解：∵函数f（x）是可导函数，且满足
，∴
∴f′（1）=-1
∴在曲线y=f（x）上的点A（1，f（1））的切线斜率是-1
故选A．
点评：本题考查导数的概念与导数的几何意义，解题的关键是正确理解导数的概念．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
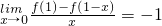，则在曲线y=f（x）上的点A（1，f（1））的切线斜率是
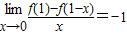，则在曲线y=f（x）上的点A（1，f（1））的切线斜率是（ ）