题目内容
16.已知D是△ABC所在平面内一点,且满足($\overrightarrow{BC}$-$\overrightarrow{CA}$)•($\overrightarrow{BD}$-$\overrightarrow{AD}$)=0,则△ABC是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
分析 利用向量的加法与减法的几何意义及平面向量数量积的运算即可判断该△ABC的形状.
解答 解:∵($\overrightarrow{BC}$-$\overrightarrow{CA}$)•($\overrightarrow{BD}$-$\overrightarrow{AD}$)=0,
∴($\overrightarrow{BC}+\overrightarrow{AC}$)•$\overrightarrow{BA}$=0,即-($\overrightarrow{CB}+\overrightarrow{CA}$)$•\overrightarrow{BA}$=0.
取AB的中点为E,
则2$\overrightarrow{CE}$•$\overrightarrow{BA}$=0,
∴CE⊥AB,E为AB的中点,
∴△ABC为等腰三角形.
故选:A.
点评 本题考查向量的加法与减法的几何意义及平面向量数量积的运算,考查三角形的形状判断,将已知条件适当变形是关键,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
6.利用计算机在区间(0,1)上产生两个随机数a和b,则关于x的方程x2+2ax+b=0有实根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
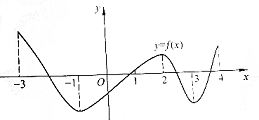 已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.
已知函数y=f(x)在区间[-3,4]上的图象如图所示,根据图象说出函数的单调区间,以及在每一个区间上函数的单调性.