题目内容
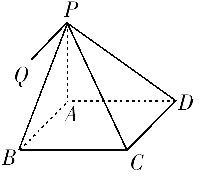
过正方形ABCD的顶点A作线段A′A⊥平面ABCD．若A′A=AB，则平面A′AB与平面A′CD所成角的度数是（ ）
分析：根据二面角的平面角的定义可知在平面A′AB内，过点A′作A′Q∥AB，则A′Q为平面A′AB和平面A′CD所成二面角的棱，然后可证得，A′A⊥A′Q，A′D⊥A′Q，则∠AA′D为所求角，在Rt△AA′D中可求得此角即可．
解答：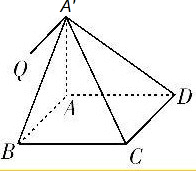
解答：解：如图，考虑与平面A′AB和平面A′CD同时相交的第三平面ABCD，
其交线为AB和CD，而AB∥CD，
则平面A′AB和平面A′CD所成二面角的棱必与AB，CD平行．
在平面A′AB内，过点P作A′Q∥AB，
则A′Q为平面A′AB和平面A′CD所成二面角的棱，
然后可证得，A′A⊥A′Q，A′D⊥A′Q，
∠AA′D为所求角，在Rt△AA′D中可求得，∠AA′D=45°．
故选B
解答：解：如图，考虑与平面A′AB和平面A′CD同时相交的第三平面ABCD，其交线为AB和CD，而AB∥CD，
则平面A′AB和平面A′CD所成二面角的棱必与AB，CD平行．
在平面A′AB内，过点P作A′Q∥AB，
则A′Q为平面A′AB和平面A′CD所成二面角的棱，
然后可证得，A′A⊥A′Q，A′D⊥A′Q，
∠AA′D为所求角，在Rt△AA′D中可求得，∠AA′D=45°．
故选B
点评：点评：本题中两平面与第三平面分别有一条相交直线，这两条直线平行，由线面平行的判定和性质知，两条直线必与两平面的交线平行，由此可作出棱，从而找出二面角的平面角．本题也可补形化得正方体，利用定义，找出二面角的平面角．
练习册系列答案
名校课堂系列答案
相关题目
