题目内容
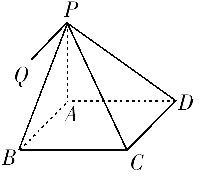
过正方形ABCD的顶点A作PA⊥平面ABCD,设PA=AB=a,求二面角BPCD的大小.
解析:∵PA⊥平面ABCD，BD⊥AC，
∴BD⊥PC.
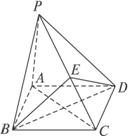
在平面PBC内作BE⊥PC于点E，连结DE，得PC⊥平面BED，从而DE⊥PC，即∠BED是二面角BPCD的平面角.
在Rt△PAB中，
由PA=AB=a,得PB=
.
∵PA⊥平面ABCD，BC⊥AB，
∴BC⊥PB.∴PC=
.
在Rt△PBC中，BE=
.
同理,DE=
.
在△BDE中，
cos∠BED=
=
,
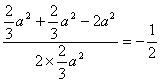∴∠BED=120°，即二面角BPCD的大小为120°.
练习册系列答案
名校课堂系列答案
相关题目
