题目内容
18.设sinα是sinθ,cosθ的等差中项,sinβ是sinθ,cosθ的等比中项,求证:cos4β-4cos4α=3.分析 所证明的式子中不含角θ,因此先由已知,考虑将θ作为桥梁,沟通α,β,得出4sin2α-2sin2β=1.再由降幂公式证明等式左边等于右边即可.
解答 证明:∵由题意,sinθ+cosθ=2sinα ①,
sinθ•cosθ=sin2β ②,…(2分)
∴①2-2×②消去θ得4sin2α-2sin2β=1③.…(5分)
∴可得:4×$(\frac{1-cos2α}{2})$-2×($\frac{1-cos2β}{2}$)=1,解得:2cos2α=cos2β,即4cos22α=cos22β,
∴等式左边=2cos22β-1-4(2cos22α-1)=8cos22α-1-8cos22α+4=3=右边,故得证.
点评 本题考查三角函数恒等式的证明,要求灵活运用同角三角函数间的基本关系,以及二倍角的正弦、余弦函数公式化简求值,考查了减元,转化思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.函数y=sin(π-x)-1的图象( )
| A. | 关于x=$\frac{π}{2}$对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于x=π对称 |
 如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,线段AB的中点坐标为(-2,-6).
如图,已知直线l:y=kx-2与抛物线C:x2=-2py(p>0)交于A,B两点,线段AB的中点坐标为(-2,-6).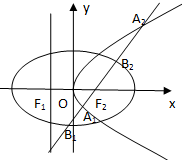 设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为$\frac{1}{2}$的椭圆记作C2
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为$\frac{1}{2}$的椭圆记作C2