题目内容
17.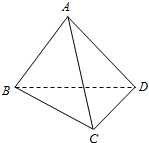 如图,四面体 ABCD的一条棱长为 x,其余棱长均为 1,记四面体 ABCD的体积为F(x),则函数F(x)的单调增区间是$(0,\frac{\sqrt{6}}{2}]$,;最大值为$\frac{1}{8}$.
如图,四面体 ABCD的一条棱长为 x,其余棱长均为 1,记四面体 ABCD的体积为F(x),则函数F(x)的单调增区间是$(0,\frac{\sqrt{6}}{2}]$,;最大值为$\frac{1}{8}$.
分析 如图所示,设BC=x,AB=AC=AD=CD=BD=1.取AD的中点O,连接OB,OC,则OB⊥AD,OC⊥AD,OB=OC=$\frac{\sqrt{3}}{2}$.又OB∩OC=O,则AD⊥平面OBC.取BC的中点E,连接OE,则OE⊥BC,可得OE,可得F(x)=$\frac{1}{3}S△OBC•AD$=$\frac{x\sqrt{3-{x}^{2}}}{12}$(0<x<$\sqrt{3}$).利用导数研究其单调性即可得出.
解答  解:如图所示,设BC=x,AB=AC=AD=CD=BD=1.
解:如图所示,设BC=x,AB=AC=AD=CD=BD=1.
取AD的中点O,
连接OB,OC,则OB⊥AD,OC⊥AD,OB=OC=$\frac{\sqrt{3}}{2}$.
又OB∩OC=O,则AD⊥平面OBC,
取BC的中点E,连接OE,则OE⊥BC,
OE=$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{x}{2})^{2}}$=$\frac{\sqrt{3-{x}^{2}}}{2}$.
∴S△OBC=$\frac{1}{2}BC•OE$=$\frac{x\sqrt{3-{x}^{2}}}{4}$.
∴F(x)=$\frac{1}{3}S△OBC•AD$
=$\frac{1}{3}×$$\frac{x\sqrt{3-{x}^{2}}}{4}$×1
=$\frac{x\sqrt{3-{x}^{2}}}{12}$(0<x<$\sqrt{3}$).
F′(x)=$\frac{3-2{x}^{2}}{12\sqrt{3-{x}^{2}}}$,
令F′(x)≥0,解得$0<x≤\frac{\sqrt{6}}{2}$,此时函数F(x)单调递增;令F′(x)<0,解得$\frac{\sqrt{6}}{2}<x<\sqrt{3}$,此时函数F(x)单调递减法.
因此当x=$\frac{\sqrt{6}}{2}$时,F(x)取得最大值,$F(\frac{\sqrt{6}}{2})$=$\frac{\frac{\sqrt{6}}{2}×\sqrt{3-(\frac{\sqrt{6}}{2})^{2}}}{12}$=$\frac{1}{8}$.
故答案分别为:$(0,\frac{\sqrt{6}}{2}]$,$\frac{1}{8}$.
点评 本题考查了利用导数研究函数的单调性极值与最值、三棱锥的体积计算公式、线面垂直的判定定理、勾股定理、等边三角形的性质,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 19 | B. | 20 | C. | 31 | D. | 22 |
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
 如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为2的菱形,平面ABC⊥平面AA1C1C,∠A1AC=60°,∠BCA=90°.
如图,在三棱柱ABC-A1B1C1中,四边形AA1C1C是边长为2的菱形,平面ABC⊥平面AA1C1C,∠A1AC=60°,∠BCA=90°.