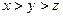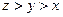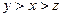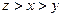题目内容
已知a>0,a2-2ab+c2=0,bc>a2.试比较a,b,c的大小.
a<c<b
∵bc>a2>0,∴b,c同号.
又a2+c2>0,a>0,∴b=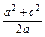 >0,∴c>0,
>0,∴c>0,
由(a-c)2=2ab-2ac=2a(b-c)≥0,∴b-c≥0.
当b-c>0,即b>c时,
由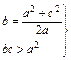 得
得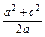 ·c>a2
·c>a2
?即(a-c)(2a2+ac+c2)<0.
∵a>0,b>0,c>0,∴2a2+ac+c2>0,
∴a-c<0,即a<c,则a<c<b;
当b-c=0,即b=c时,
∵bc>a2,∴b2>a2,即b≠a.
又∵a2-2ab+c2=(a-b)2=0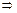 a=b与a≠b矛盾,
a=b与a≠b矛盾,
∴b-c≠0.
综上可知:a<c<b.
又a2+c2>0,a>0,∴b=
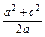 >0,∴c>0,
>0,∴c>0,由(a-c)2=2ab-2ac=2a(b-c)≥0,∴b-c≥0.
当b-c>0,即b>c时,
由
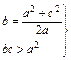 得
得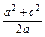 ·c>a2
·c>a2?即(a-c)(2a2+ac+c2)<0.
∵a>0,b>0,c>0,∴2a2+ac+c2>0,
∴a-c<0,即a<c,则a<c<b;
当b-c=0,即b=c时,
∵bc>a2,∴b2>a2,即b≠a.
又∵a2-2ab+c2=(a-b)2=0
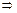 a=b与a≠b矛盾,
a=b与a≠b矛盾,∴b-c≠0.
综上可知:a<c<b.

练习册系列答案
相关题目
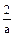 )+1(a>0,a≠1)
)+1(a>0,a≠1)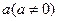 和
和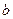 ,不等式
,不等式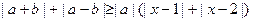 恒成立,则实数
恒成立,则实数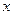 的取值范围是 .
的取值范围是 .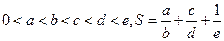 ,则把变量________的值增加1会使
,则把变量________的值增加1会使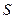 的值增加最大(填入
的值增加最大(填入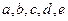 中的某个字母).
中的某个字母).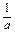 的大小.
的大小.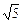 ,b=
,b=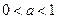 ,
,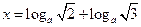 ,
,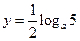 ,
,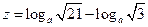 ,则( )
,则( )