题目内容
若f(x)是R上的减函数,且f(x)的图象经过点A(0,4)和点B(3,-2),则不等式|f(x+a)-1|<3的解集为(-1,2)时,a的值为
| A.0 | B.-1 |
| C.1 | D.-2 |
C
由|f(x+a)-1|<3,得-2<f(x+a)<4.
由题设可知f(0)=4,f(3)=-2.
所以f(3)<f(x+a)<f(0).
又因f(x)是R上的减函数,所以0<x+a<3,
即-a<x<3-a. ①
因不等式的解为-1<x<2, ②
所以比较①②可得a=1.
由题设可知f(0)=4,f(3)=-2.
所以f(3)<f(x+a)<f(0).
又因f(x)是R上的减函数,所以0<x+a<3,
即-a<x<3-a. ①
因不等式的解为-1<x<2, ②
所以比较①②可得a=1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则a的取值范围是
,则a的取值范围是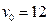 m/s竖直上抛一排球,该排球能够在地面
m/s竖直上抛一排球,该排球能够在地面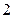 m以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离地面的高度
m以上的位置最多停留多长时间?(注:若不计空气阻力,则竖直上抛的物体距离地面的高度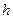 与时间
与时间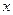 满足关系
满足关系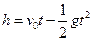 ,其中
,其中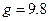 m/s
m/s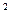 .)
.)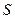 的扇形中,半径是多少时房间形的周长最小?
的扇形中,半径是多少时房间形的周长最小? ②sin2x+
②sin2x+ ≥4 ③设x,y都是正数,若
≥4 ③设x,y都是正数,若 =1,则x+y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.
=1,则x+y的最小值是12 ④若|x-2|<ε,|y-2|<ε,则|x-y|<2ε,其中所有真命题的序号是__________.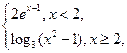
 则不等式f(x)>2的解集为
则不等式f(x)>2的解集为 (3,+∞)
(3,+∞)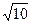 ,+∞)
,+∞)
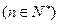 ,假设
,假设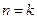 时成立,当
时成立,当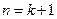 时,左端增加的项数是( ).
时,左端增加的项数是( ). 项
项 项
项 项
项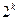 项
项