题目内容
(Ⅰ)求经过点(1,-7)与圆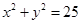 相切的切线方程.
相切的切线方程.
(Ⅱ)直线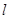 经过点P(5,5)且和圆C:
经过点P(5,5)且和圆C: 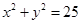 相交,截得弦长为
相交,截得弦长为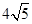 ,求
,求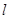 的方程.
的方程.
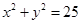 相切的切线方程.
相切的切线方程.(Ⅱ)直线
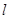 经过点P(5,5)且和圆C:
经过点P(5,5)且和圆C: 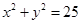 相交,截得弦长为
相交,截得弦长为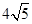 ,求
,求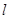 的方程.
的方程.( 1):切线方程为:4x-3y-25 = 0或3x + 4y + 25 =" 0" .
(2).解:直线 的方程为:x-2y +5 = 0或2x-y-5=0.
(2).解:直线 的方程为:x-2y +5 = 0或2x-y-5=0.
本试题主要是考查了直线与圆的位置关系的运用。
(1)设切线的斜率为k,由点斜式有:y +7 =" k(x-" 1),即y =" k(x-" 1) –7代入圆方程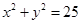 得:
得: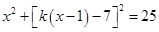 则判别式等于零,得到k的值。
则判别式等于零,得到k的值。
(2)因为 是圆心到直线
是圆心到直线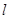 的距离,
的距离,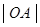 是圆的半径,
是圆的半径,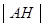 是弦长
是弦长 的一半,在
的一半,在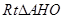 中,
中,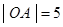 ,
,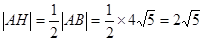 ,那么在
,那么在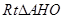 中,利用勾股定理得到结论。
中,利用勾股定理得到结论。
(1)设切线的斜率为k,由点斜式有:y +7 =" k(x-" 1),即y =" k(x-" 1) –7代入圆方程
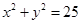 得:
得: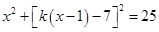 则判别式等于零,得到k的值。
则判别式等于零,得到k的值。(2)因为
 是圆心到直线
是圆心到直线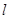 的距离,
的距离,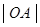 是圆的半径,
是圆的半径,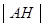 是弦长
是弦长 的一半,在
的一半,在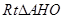 中,
中,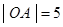 ,
,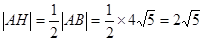 ,那么在
,那么在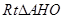 中,利用勾股定理得到结论。
中,利用勾股定理得到结论。
练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 的图像相切于点
的图像相切于点 ,且
,且 ,
, 为坐标原点,
为坐标原点, 为图像的极大值点,与
为图像的极大值点,与 轴交于点
轴交于点 ,过切点
,过切点 ,则
,则 =
=


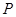 在直线
在直线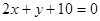 上
上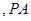 、
、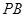 与圆
与圆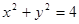 分别相切于
分别相切于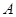 、
、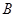 两点
两点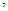 则四边形
则四边形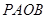 的面积的最小值为( )
的面积的最小值为( )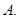
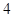
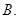
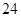
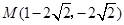 射到
射到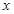 轴上,再反射到圆
轴上,再反射到圆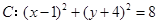 上,求反射点在
上,求反射点在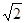 ,0)
,0)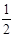 ,则m+n= .
,则m+n= .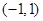 且斜率为
且斜率为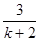 的直线
的直线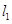 与直线
与直线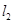 :
: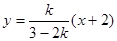 平行,则实数
平行,则实数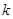 的值为( )
的值为( ) 过点
过点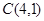 , (1)若直线
, (1)若直线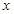 轴、y轴的正半轴相交于
轴、y轴的正半轴相交于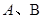 两点,O为坐标原点,记
两点,O为坐标原点,记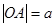
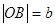 ,求
,求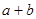 的最小值,并写出此时直线
的最小值,并写出此时直线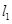 :
: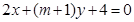 与直线
与直线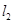 :
: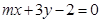 平行,则m的值为
平行,则m的值为