Question

已知函数f（x）=

1-|x|

x

，分别给出下面几个结论：①f（x）是奇函数；②函数f（x）的值域为R；③函数f（x）有两个零点；④若f（x）=m有一解，则m＞1．其中正确结论的序号有

①②③

．（请将你认为正确的结论的序号都填上）

Answer 1

分析：（1）用奇偶性的定义即可判断①是否正确
（2）画出函数图象，数形结合，即可判断②是否正确
（3）令f（x）=0解方程即可判断③是否正确
（4）画函数图象，数形结合即可判断④是否正确

解答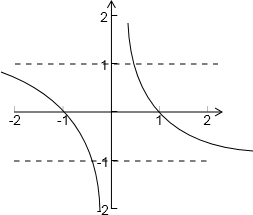：解：由题意知f(x)=

1 x -1  ， x＞0 1 x +1 ， x＜0

根据图象变换和y=

1

x

的图象，画出原函数图象如图：
（1）f（x）的定义域为（-∞，0）∪（0，+∞），
又f(-x)=

1-|-x|

-x

=-

1-|x|

x

=-f(x)
∴f（x）是奇函数
∴①正确
（2）当x＞0时，f（x）＞-1
当x＜0时，f（x）＜1
∴f（x）的值域为R
∴②正确
（3）令f（x）=0，解得x=-1或x=1
∴函数f（x）有两个零点
∴③正确
（4）由图象知，若f（x）=m有一解，则m≤-1或m≥1
∴④不正确
故答案为：①②③

点评：本题综合考查函数的图象、性质及函数的零点，注意数形结合思想和函数与方程思想的应用．属简单题