题目内容
(本小题满分l2分)
若集合A＝{x|x2－2x－8＜0}，B＝{x|x－m＜0}．
(1)若m＝3，试求A∩(∁RB)；
(2)若A∩B＝∅，求实数m的取值范围；
(3)若A∩B＝A，求实数m的取值范围．
【答案】
解：(1)由x2－2x－8<0，得－2<x<4，∴A＝{x|－2<x<4}．
当m＝3时，由x－m<0，得x<3，∴B＝{x|x<3}，
∴U＝A∪B＝{x|x<4}，∁UB＝{x|3≤x<4}．
∴A∩(∁UB)＝{x|3≤x<4}．
(2)∵A＝{x|－2<x<4}，B＝{x|x<m}，
又A∩B＝∅，∴m≤－2.
(3)∵A＝{x|－2<x<4}，B＝{x|x<m}，
由A∩B＝A，得A⊆B，∴m≥4.
【解析】略
练习册系列答案
相关题目
，bn＋1＝－
Sn（n∈N*）．
＋
＋…＋
，求Tn的表达式
，过左焦点
作直线
与椭圆交于点P，Q，直线AP，AQ分别与直线
交于点
．
为直径的圆经过焦点
．
：函数
（
）的值域是
；命题
：指数函数
在
上是减函数．若命题“
的范围．
并且与曲线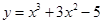
相切的直线方程.