题目内容
(本小题满分l2分)已知椭圆的的右顶点为A,离心率 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段 为直径的圆经过焦点
为直径的圆经过焦点 .
.
【答案】
(Ⅰ)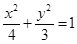
(Ⅱ)见解析
【解析】(Ⅰ)解: 由已知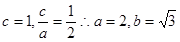
∴ 椭圆方程为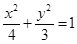 .——————————5分
.——————————5分
(Ⅱ) 设直线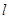 方程为y=k(x+1),
方程为y=k(x+1),
由 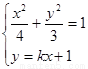 得
得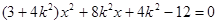 .
.
设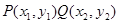 ,则
,则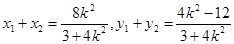 .—————7分
.—————7分
设 ,则由A,P,M共线,得
,则由A,P,M共线,得
 同理
同理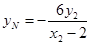 .
.
∴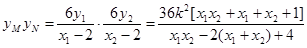 .——————9分
.——————9分
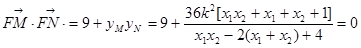
∴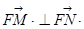 ,即
,即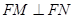 ,以线段MN为直径的圆经过点F;
,以线段MN为直径的圆经过点F;
当直线L的斜率不存在时,不妨设M(-4,3).N(-4,-3),则有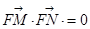 ,
,
∴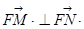 ,即
,即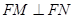 ,以线段MN为直径的圆经过点F.
,以线段MN为直径的圆经过点F.
综上所述,以线段MN为直径的圆经过定点F. ———————————12分

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线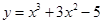 相切的直线方程.
相切的直线方程.