题目内容
如图,液体从一圆锥漏斗漏入一圆柱桶中,开始漏斗盛满液体,经过3分钟漏完,若圆柱中液面上升速度是一常量, H是圆锥漏斗中液面下落的距离. 则H与下落时间t分钟的函数关系表示的图象可能是( )
B
解析试题分析:利用特殊值法,圆柱液面上升速度是常量,表示圆锥漏斗中液体单位时间内落下的体积相同,当时间取1.5分钟时,液面下降高度与漏斗高度的 比较.由于所给的圆锥形漏斗上口大于下口,当时间取
比较.由于所给的圆锥形漏斗上口大于下口,当时间取 t时,漏斗中液面下落的高度不会达到漏斗高度的
t时,漏斗中液面下落的高度不会达到漏斗高度的 ,对比四个选项的图象可得结果.故选B
,对比四个选项的图象可得结果.故选B
考点:本题考查函数的图像.
点评:本题考查函数图象,还可以正面分析得出结论:圆柱液面上升速度是常量,则V(这里的V是漏斗中剩下液体的体积)与t成正比(一次项),根据圆锥体积公式V=  ,可以得出H=at2+bt中,a为正数,另外,t与r成反比,可以得出H=at^2+bt中,b为正数.所以选择第二个答案.
,可以得出H=at2+bt中,a为正数,另外,t与r成反比,可以得出H=at^2+bt中,b为正数.所以选择第二个答案.

练习册系列答案
相关题目
直角梯形ABCD如图(1),动点P从B点出发,由B→C→D→A沿边运动,设点P运动的距离为x,ΔABP面积为f(x).若函数y= f(x)的图象如图(2),则ΔABC的面积为 ( )
| A.10 | B.16 | C.18 | D.32 |
函数 的零点所在的区间为( )
的零点所在的区间为( )
| A.(-1,0) | B.( ,1) ,1) | C.(1,2) | D.(1, ) ) |
设奇函数 上是增函数,且
上是增函数,且 ,则不等式
,则不等式 的解集为( )
的解集为( )
A.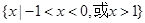 | B.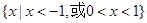 |
C. | D. |
函数 的零点所在的区间是 ( )
的零点所在的区间是 ( )
A. | B. | C. | D. |
将方程 的正根从小到大地依次排列为
的正根从小到大地依次排列为 ,给出以下不等式:
,给出以下不等式:
① ;②
;② ;③
;③ ;④
;④ ;
;
其中,正确的判断是( )
| A.①③ | B.①④ | C.②③ | D.②④ |
已知函数 是定义在
是定义在 上的偶函数. 当
上的偶函数. 当 时,
时, ,则当
,则当 时,函数
时,函数 的解析式为 ( )
的解析式为 ( )
A. | B. | C. | D. |
 与曲线
与曲线 有四个交点,则
有四个交点,则 的取值范围是
的取值范围是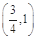 B.
B. C.
C. D.
D.
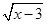 +
+ 是函数;
是函数; 与g(x)=x是同一函数.
与g(x)=x是同一函数.