题目内容
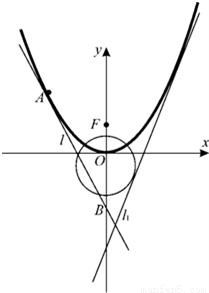
已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.(1)求m与a的值;
(2)设A是C1上的一动点,以A为切点的C1的切线l交y轴于点B,设
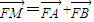 ,证明:点M在一定直线上.
,证明:点M在一定直线上.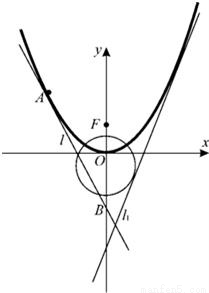
【答案】分析:(1)利用圆心到直线的距离等于半径求出m,再利用导函数与切线的关系求出a的值即可.
(2)先求出以A为切点的切线l的方程以及点A,B的表达式,再求出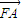 ,
,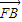 ,利用
,利用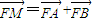 即可求出点M所在的定直线.
即可求出点M所在的定直线.
解答:解:(1)由已知,圆C2:x2+(y+1)2=5的圆心为C2(0,-1),半径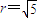 .(1分)
.(1分)
由题设圆心到直线l1:y=2x+m的距离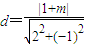 .(3分)
.(3分)
即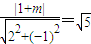 ,
,
解得m=-6(m=4舍去).(4分)
设l1与抛物线的相切点为A(x,y),又y′=2ax,(5分)
得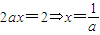 ,
,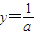 .(6分)
.(6分)
代入直线方程得: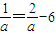 ,∴
,∴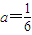
所以m=-6,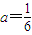 .(7分)
.(7分)
(2)由(1)知抛物线C1方程为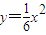 ,焦点
,焦点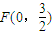 .(8分)
.(8分)
设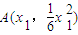 ,由(1)知以A为切点的切线l的方程为
,由(1)知以A为切点的切线l的方程为 .(10分)
.(10分)
令x=0,得切线l交y轴的B点坐标为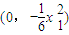 (11分)
(11分)
所以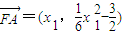 ,
,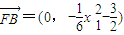 ,(12分)
,(12分)
∴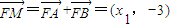 (13分)
(13分)
因为F是定点,所以点M在定直线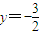 上.(14分)
上.(14分)
点评:本题是对圆与椭圆知识的综合考查.当直线与圆相切时,可以利用圆心到直线的距离等于半径求解.,也可以把直线与圆的方程联立让对应方程的判别式为0求解.本题用的是第一种.
(2)先求出以A为切点的切线l的方程以及点A,B的表达式,再求出
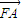 ,
,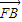 ,利用
,利用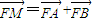 即可求出点M所在的定直线.
即可求出点M所在的定直线.解答:解:(1)由已知,圆C2:x2+(y+1)2=5的圆心为C2(0,-1),半径
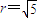 .(1分)
.(1分)由题设圆心到直线l1:y=2x+m的距离
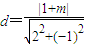 .(3分)
.(3分)即
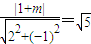 ,
,解得m=-6(m=4舍去).(4分)
设l1与抛物线的相切点为A(x,y),又y′=2ax,(5分)
得
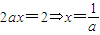 ,
,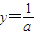 .(6分)
.(6分)代入直线方程得:
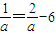 ,∴
,∴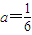
所以m=-6,
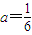 .(7分)
.(7分)(2)由(1)知抛物线C1方程为
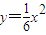 ,焦点
,焦点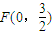 .(8分)
.(8分)设
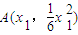 ,由(1)知以A为切点的切线l的方程为
,由(1)知以A为切点的切线l的方程为 .(10分)
.(10分)令x=0,得切线l交y轴的B点坐标为
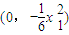 (11分)
(11分)所以
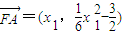 ,
,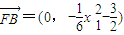 ,(12分)
,(12分)∴
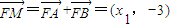 (13分)
(13分)因为F是定点,所以点M在定直线
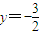 上.(14分)
上.(14分)点评:本题是对圆与椭圆知识的综合考查.当直线与圆相切时,可以利用圆心到直线的距离等于半径求解.,也可以把直线与圆的方程联立让对应方程的判别式为0求解.本题用的是第一种.

练习册系列答案
相关题目
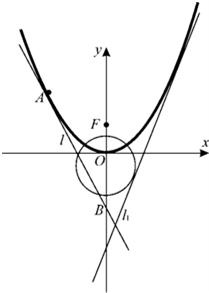 已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.
已知抛物线C1的方程为y=ax2(a>0),圆C2的方程为x2+(y+1)2=5,直线l1:y=2x+m(m<0)是C1、C2的公切线.F是C1的焦点.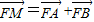 ,证明:点M在一定直线上.
,证明:点M在一定直线上.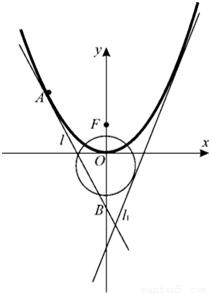
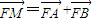 ,证明:点M在一定直线上.
,证明:点M在一定直线上.