题目内容
点P在椭圆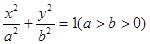 上,椭圆的左准线为直线l,左焦点为F,作PQ⊥l于点Q,若P、F、Q三点构成一个等腰直角三角形,则该椭圆的离心率为
上,椭圆的左准线为直线l,左焦点为F,作PQ⊥l于点Q,若P、F、Q三点构成一个等腰直角三角形,则该椭圆的离心率为
【答案】
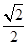
【解析】
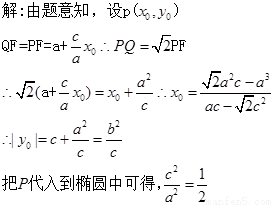
故离心率为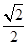

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
点P在椭圆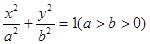 上,椭圆的左准线为直线l,左焦点为F,作PQ⊥l于点Q,若P、F、Q三点构成一个等腰直角三角形,则该椭圆的离心率为
上,椭圆的左准线为直线l,左焦点为F,作PQ⊥l于点Q,若P、F、Q三点构成一个等腰直角三角形,则该椭圆的离心率为
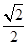
【解析】
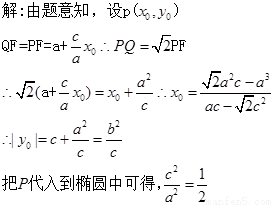
故离心率为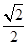

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案