题目内容
已知椭圆
的中心在坐标原点，焦点在
轴上且过点
，离心率是
．
（1）求椭圆
的标准方程；
（2）直线过点
且与椭圆交于
，
两点，若
，求直线的方程.
（1）
；（2）
和
．
【解析】
试题分析：（1）由题设条件知关于a,b,c的方程组，由此能求出椭圆方程．
（2）可以设直线方程（斜率不存在单独考虑），然后与椭圆方程联立，消去y得到关于x的一元二次方程，利用韦达定理结合题目条件建立方程即可求出直线方程.
试题解析：（1）设椭圆
的方程为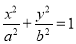
.
由已知可得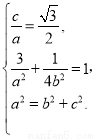
3分
解得
，
.
故椭圆
的方程为． 6分
（2）由已知，若直线的斜率不存在，则过点
的直线的方程为
，
此时
，显然
不成立． 7分
若直线的斜率存在，则设直线的方程为
．
则
整理得
． 9分
由
．
设
．
故
，① 
． ② 10分
因为，即
．③
①②③联立解得
． 13分
所以直线的方程为和． 14分
考点：(1)椭圆标准方程；（2）直线与圆锥曲线的位置关系.
练习册系列答案
相关题目
甲乙两个班级均为40人，进行一门考试后，按学生考试成绩及格与不及格进行统计，甲班及格人数为36人，乙班及格人数为24人. 根据以上数据建立一个
的列联表如下：
| 不及格 | 及格 | 总计 |
甲班 | a | b |
|
乙班 | c | d |
|
总计 |
|
|
|
参考公式：
；
P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
根据以上信息，在答题卡上填写以上表格，通过计算对照参考数据，有_____的把握认为“成绩与班级有关系” ．
