题目内容
(本题满分16分,第(1)小题8分,第(2)小题8分)
己知双曲线的中心在原点,右顶点为![]()
![]() (1,0),点
(1,0),点![]() 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点![]() (
(![]() ,0)到直线
,0)到直线![]() 的距离为1.
的距离为1.
(1)若直线![]() 的斜率为
的斜率为![]() 且有
且有 ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]()
![]() 的内心恰好是点
的内心恰好是点![]() ,求此双曲线的方程.
,求此双曲线的方程.
(Ⅰ) ![]() 或
或![]() ; (Ⅱ)
; (Ⅱ) ![]()
解析:
设直线![]() 的方程为:
的方程为:![]() ,…………………2分
,…………………2分
由点![]() 到直线
到直线![]() 的距离为
的距离为![]() 可知:
可知:
![]() 得到
得到 ,…………………5分
,…………………5分
因为![]() ,所以
,所以![]()
![]() ,
,
所以 ![]() ,
,![]() 或
或![]()
所以 ![]() 或
或![]() ;…………………8分
;…………………8分
(2)当![]() 时,
时,![]() ,
,
由于点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,所以直线
,所以直线![]() 的斜率
的斜率![]() ,……10分
,……10分
因为点![]() 为
为![]() 的内心,故
的内心,故![]() 是双曲线上关于
是双曲线上关于![]() 轴对称的两点,所以
轴对称的两点,所以![]() 轴,不妨设直线
轴,不妨设直线![]() 交
交![]() 轴于点
轴于点![]() ,则
,则![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,…………………12分
,…………………12分
所以![]() 两点的横坐标均为
两点的横坐标均为![]() ,把
,把![]() 代入直线
代入直线![]() 的方程:
的方程:![]() ,得
,得![]() ,所以
,所以![]() 两点的坐标分别为:
两点的坐标分别为:![]() ,
,
设双曲线方程为:![]() ,把点
,把点![]() 的坐标代入方程得到
的坐标代入方程得到
![]() ,…………………15分
,…………………15分
所以双曲线方程为:![]() …………………16分
…………………16分

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,
,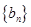 是等差数列,且
是等差数列,且 ,求非零常数
,求非零常数 ;
; ,求证:
,求证: .
.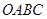 中,已知过点
中,已知过点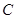 的直线与线段
的直线与线段 分别相交于点
分别相交于点 。若
。若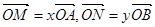 。
。 与
与 的关系为
的关系为 ;
; ,定义在
,定义在 上的偶函数
上的偶函数 ,当
,当 时
时 ,且函数
,且函数 对称,求证:
对称,求证: ,并求
,并求 时的解析式;
时的解析式; 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围。
的取值范围。 、
、 为坐标平面
为坐标平面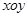 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点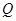 (异于
(异于 ,点
,点 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
; 在椭圆
在椭圆 上,试问:点
上,试问:点 、
、 是圆
是圆 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 是
是 轴正方向的单位向量,设
轴正方向的单位向量,设 =
= ,
,  =
= ,且满足
,且满足 .
.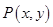 的轨迹方程;
的轨迹方程; 的直线
的直线 交上述轨迹于
交上述轨迹于 两点,且
两点,且 ,求直线
,求直线