题目内容
从9名学生中选出4人参加辩论赛,其中甲、乙、丙三人至少有两人入选的不同选法的种数为( )
| A.36 | B.51 | C.63 | D.96 |
B
解析试题分析:由题意9名学生中选出4人参加辨论比赛,其中甲、乙、丙三人至少有两人入选的不同选法有两类,
一类是三人中有两人参加,入选种数为C32×C62=45,
一类是三人都参加,入选种数为C33×C61=6,
所以总的入选种数有45+6=51,故选B。
考点:计数原理,简单组合应用问题。
点评:简单题,排列组合应用问题,关键是首先区分是排列,还是组合应用问题,主要看“顺序的有无” , 此类问题,往往与计数原理相结合,分类或分步解决问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若x为自然数,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
由数字0,1,2,3,4,5组成的奇偶数字相间且无重复数字的六位数的个数是
| A.36 | B.48 | C.60 | D.72 |
若 ,则
,则 等于()
等于()
A. | B. | C. | D. |
甲、乙等5人站成一排,其中甲、乙不相邻的不同排法共有( )
| A.144种 | B.72种 | C.36 种 | D.12种 |
现有四件不同款式的上衣与三件不同颜色的长裤,如果一条长裤与一件上衣配成一套,则不同的选法数为
| A.7 | B.64 | C.12 | D.81 |

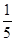
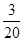

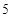 架舰载机准备着舰,如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )
架舰载机准备着舰,如果甲、乙两机必须相邻着舰,而丙、丁两机不能相邻着舰,那么不同的着舰方法有( )