题目内容
甲、乙等5人站成一排，其中甲、乙不相邻的不同排法共有（ ）
| A．144种 | B．72种 | C．36 种 | D．12种 |
B
解析试题分析：根据题意，由于甲、乙等5人站成一排，所有的情况有
,而对于甲、乙相邻的情况有
，那么可知不相邻的情况有-=72，选B.
考点：排列与组合
点评：本题主要考查排列与组合及两个基本原理，求出甲、乙两人恰好相邻的方法数为A22•A44，是解题的关键．
练习册系列答案
星级口算天天练系列答案
相关题目
6名同学从左到右站成一排，其中甲不能站在两头，不同的站法有（ ）种
| A．480 | B．240 | C．120 | D．96 |
从9名学生中选出4人参加辩论赛，其中甲、乙、丙三人至少有两人入选的不同选法的种数为（ ）
| A．36 | B．51 | C．63 | D．96 |
5人站成一排，甲乙之间恰有一个人的站法有（ ）.
| A．18 | B．24 | C．36 | D．48 |
设服从二项分布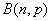
的随机变量
的期望与方差分别是
和
，则
、
的值分别是（ ）．
A． | B． | C． | D． |
8名学生和2位第师站成一排合影，2位老师不相邻的排法种数为（ ）
A． | B． | C． | D． |
若
则
（ ）
A． | B． | C． | D． |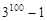
将5名实习老师全部分配到高三年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（ ）
| A．30种 | B．90种 | C．180种 | D．270种 |