题目内容
设单调递增等比数列{an}满足a1+a2+a3=7,且a3是a1,a2+5的等差中项,(1)求数列{an}的通项;
(2)数列{cn}满足:对任意正整数n,
| c1 |
| a1 |
| c2 |
| a2 |
| cn |
| an |
| 2n-11 |
| 2n-1 |
分析:(1)将已知条件a1+a2+a3=7,且a3是a1,a2+5的等差中项,用基本量表示,列出方程组,求出首项与公比,利用等比数列的通项公式求出数列{an}的通项.
(2)根据已知等式仿写出新等式
+
+…+
=22+
,两式相减求出数列{cn}的通项,利用等差数列的前n项和公式求出数列{cn}的前n项和.
(2)根据已知等式仿写出新等式
| c1 |
| a1 |
| c2 |
| a2 |
| cn-1 |
| an-1 |
| 2n-13 |
| 2n-2 |
解答:解:(1)设等比数列{an}的公比为q,则
,
两式相减,得a1q2=4,(3分)
代入第一方程得
+
+4=7,
解得q=2或q=-
(舍),
又a1=1,
所以an=2n-1(6分)
(2)对任意正整数n,
+
+…+
=22+
均成立,
n=1时,c1=13(8分)
当n≥2时,
+
+…+
=22+
,
两式相减得
=
-
=
所以n≥2时,cn=15-2n,
n=1也满足此式 (12分)
∴Sn=
=-n2+14n(14分)
|
两式相减,得a1q2=4,(3分)
代入第一方程得
| 4 |
| q2 |
| 4 |
| q |
解得q=2或q=-
| 2 |
| 3 |
又a1=1,
所以an=2n-1(6分)
(2)对任意正整数n,
| c1 |
| a1 |
| c2 |
| a2 |
| cn |
| an |
| 2n-11 |
| 2n-1 |
n=1时,c1=13(8分)
当n≥2时,
| c1 |
| a1 |
| c2 |
| a2 |
| cn-1 |
| an-1 |
| 2n-13 |
| 2n-2 |
两式相减得
| cn |
| an |
| 2n-11 |
| 2n-1 |
| 2n-13 |
| 2n-2 |
| 15-2n |
| 2n-1 |
所以n≥2时,cn=15-2n,
n=1也满足此式 (12分)
∴Sn=
| (13+15-2n)n |
| 2 |
点评:解决等差数列、等比数列的有关问题,一般利用通项公式及前n项和公式列出方程组,求出基本量,然后在解决.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
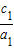 +
+ +…+
+…+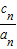 =22+
=22+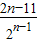 均成立,求数列{cn}的前n项和.
均成立,求数列{cn}的前n项和.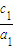 +
+ +…+
+…+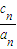 =22+
=22+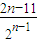 均成立,求数列{cn}的前n项和.
均成立,求数列{cn}的前n项和.