题目内容
知双曲线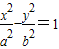 的离心率为e.
的离心率为e.(1)集合
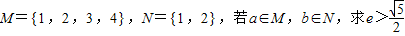 的概率;
的概率;(2)若0<a<4,0<b<2,求e>
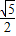 的概率.
的概率.
【答案】分析:(1)从M中任取一数为a,从N中任取一数为b,通过列举得到共8种情况,而事件“双曲线的离心率e>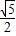 ”对应
”对应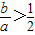 ,符合条件的有(3,1),(4,1)两种情况,用随机事件的概率公式,可得所求的概率;
,符合条件的有(3,1),(4,1)两种情况,用随机事件的概率公式,可得所求的概率;
(2)作出aob坐标系如图,得事件“0<a<4,0<b<2”对应的图形是长为4,宽为2的长方形区域,而事件B对应的点(a,b)位于矩形右下方的半个三角形,即图中阴影部分,最后用几何概型的公式,相除即得所求的概率.
解答: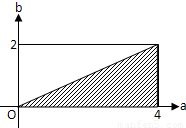 解:(1)从M任取一数为a,从N中任取一数为b,有(1,1),(1,2),
解:(1)从M任取一数为a,从N中任取一数为b,有(1,1),(1,2),
(2,1),(2,2),(3,1),(3,2),(4,1),(4,2)共8种情况
记事件A=“双曲线的离心率e>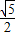 ”,则
”,则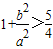 ,
,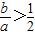 ,符合条件的有(3,1),(4,1)两种情况,
,符合条件的有(3,1),(4,1)两种情况,
∴所求的概率为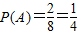
(2)集合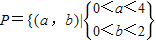 ,P对应的图形是长为4,宽为2的长方形区域(如图),其面积S1=8,
,P对应的图形是长为4,宽为2的长方形区域(如图),其面积S1=8,
记事件B={双曲线的离心率e>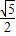 },则a<2b,满足条件的点(a,b)位于图中阴影部分,其面积S2=4,
},则a<2b,满足条件的点(a,b)位于图中阴影部分,其面积S2=4,
∴所求的概率为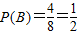
点评:本题从两个集合中分别取一个元素,作为双曲线的实半轴和虚半轴,求双曲线离心率大于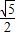 的概率,着重考查了双曲线的离心率和随机事件的概率等知识点,属于基础题.
的概率,着重考查了双曲线的离心率和随机事件的概率等知识点,属于基础题.
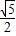 ”对应
”对应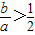 ,符合条件的有(3,1),(4,1)两种情况,用随机事件的概率公式,可得所求的概率;
,符合条件的有(3,1),(4,1)两种情况,用随机事件的概率公式,可得所求的概率;(2)作出aob坐标系如图,得事件“0<a<4,0<b<2”对应的图形是长为4,宽为2的长方形区域,而事件B对应的点(a,b)位于矩形右下方的半个三角形,即图中阴影部分,最后用几何概型的公式,相除即得所求的概率.
解答:
 解:(1)从M任取一数为a,从N中任取一数为b,有(1,1),(1,2),
解:(1)从M任取一数为a,从N中任取一数为b,有(1,1),(1,2),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2)共8种情况
记事件A=“双曲线的离心率e>
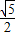 ”,则
”,则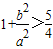 ,
,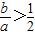 ,符合条件的有(3,1),(4,1)两种情况,
,符合条件的有(3,1),(4,1)两种情况,∴所求的概率为
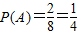
(2)集合
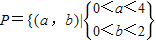 ,P对应的图形是长为4,宽为2的长方形区域(如图),其面积S1=8,
,P对应的图形是长为4,宽为2的长方形区域(如图),其面积S1=8,记事件B={双曲线的离心率e>
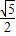 },则a<2b,满足条件的点(a,b)位于图中阴影部分,其面积S2=4,
},则a<2b,满足条件的点(a,b)位于图中阴影部分,其面积S2=4,∴所求的概率为
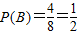
点评:本题从两个集合中分别取一个元素,作为双曲线的实半轴和虚半轴,求双曲线离心率大于
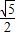 的概率,着重考查了双曲线的离心率和随机事件的概率等知识点,属于基础题.
的概率,着重考查了双曲线的离心率和随机事件的概率等知识点,属于基础题. 
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 的离心率为e,左、右两焦点分别为F1、F2,焦距为
的离心率为e,左、右两焦点分别为F1、F2,焦距为 ,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)
,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)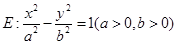 的离心率为e,左、右两焦点分别为F1、F2,焦距为
的离心率为e,左、右两焦点分别为F1、F2,焦距为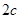 ,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)
,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为 (
)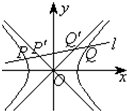 已知双曲线
已知双曲线 的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ.
的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ.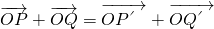 .
.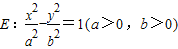 的离心率为e,左、右两焦点分别为F1、F2,焦距为2c,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为( )
的离心率为e,左、右两焦点分别为F1、F2,焦距为2c,抛物线C以F2为顶点,F1为焦点,点P为抛物线与双曲线右支上的一个交点,若a|PF2|+c|PF1|=8a2,则e的值为( )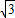
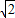
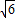
 的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ.
的离心率为e,右顶点为A,左、右焦点分别为F1、F2,点E为右准线上的动点,∠AEF2的最大值为θ. .
.