题目内容
如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为中线DE上一点,且DG=2GE,则AG= .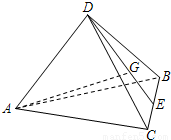
【答案】分析:利用勾股定理、余弦定理,计算BC,DB,DC的值,从而可求cos∠ADG,在△ADG中,利用余弦定理,可求AG.
解答:解:∵AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,
∴BC=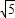 ,DB=
,DB=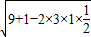 =
=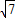 ,DC=
,DC=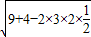 =
=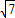
∴DE=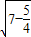 =
=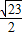 ,AE=
,AE=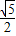
∴cos∠ADG= =
=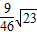
∵DG=2GE,
∴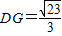
∴在△ADG中,AG=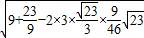 =
=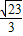
故答案为: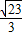
点评:本题考查空间距离的计算,考查余弦定理的运用,考查学生的计算能力,属于中档题.
解答:解:∵AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,
∴BC=
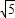 ,DB=
,DB=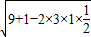 =
=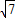 ,DC=
,DC=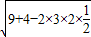 =
=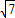
∴DE=
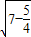 =
=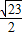 ,AE=
,AE=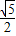
∴cos∠ADG=
 =
=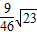
∵DG=2GE,
∴
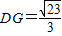
∴在△ADG中,AG=
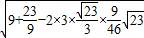 =
=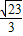
故答案为:
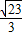
点评:本题考查空间距离的计算,考查余弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
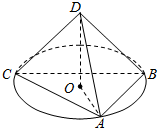 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
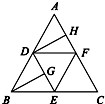 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为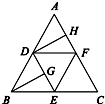 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )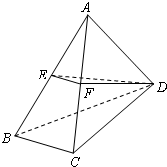 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.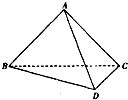 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中,