题目内容
 如图,抛物线形拱桥的顶点距水面2米时,测得拱 桥内水面宽为12米,当水面升高1米后,则拱桥内水面的宽度为
如图,抛物线形拱桥的顶点距水面2米时,测得拱 桥内水面宽为12米,当水面升高1米后,则拱桥内水面的宽度为6
| 2 |
6
米.| 2 |
分析:先根据题目条件建立直角坐标系,设出抛物线的方程,然后利用点在曲线上,确定方程,求得点的坐标,也就得到水面的宽.
解答:解:以抛物线的顶点为原点,对称轴为y轴建立直角坐标系
设抛物线x2=-2py,由题意可知抛物线过点(6,-2).
点(6,-2)代入,得62=4p,解得p=9,则x2=-18y.y=-1代入,求得x=3
,
所以水面宽6
米.
故答案为:6
.
设抛物线x2=-2py,由题意可知抛物线过点(6,-2).
点(6,-2)代入,得62=4p,解得p=9,则x2=-18y.y=-1代入,求得x=3
| 2 |
所以水面宽6
| 2 |
故答案为:6
| 2 |
点评:本题考查抛物线的应用,以及待定系数法求方程,注意点在曲线上的条件的应用,是个基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
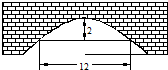 如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是多少米?
如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是多少米? 如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是( )
如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是( ) 如图,抛物线形拱桥的顶点距水面4m时,测得拱桥内水面宽为16m;当水面升高3m后,拱桥内水面的宽度为
如图,抛物线形拱桥的顶点距水面4m时,测得拱桥内水面宽为16m;当水面升高3m后,拱桥内水面的宽度为