题目内容
 如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是( )
如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是( )分析:作出如图所示直角坐标系,设抛物线方程为x2=-2py(p>0),由题意点(6,-2)在抛物线上,代入得到关于p的等式,解出p=9从而得到抛物线方程为x2=-18y,最后令y=-1算出x的值,即可得到所求拱桥内水面宽度.
解答:解: 以拱桥的顶点为原点,抛物线的轴为y轴,建立如图所求直角坐标系,
以拱桥的顶点为原点,抛物线的轴为y轴,建立如图所求直角坐标系,
设抛物线的方程为x2=-2py(p>0),
∵拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,
∴点(6,-2)在抛物线上,可得62=-2p×(-2),解得p=9
因此抛物线的方程为x2=-18y,
当水面升高1米后,水面所在直线为y=-1,
∴由x2=-18×(-1)=18,得x=±3
,可得拱桥内水面宽度是6
米.
故选:A
 以拱桥的顶点为原点,抛物线的轴为y轴,建立如图所求直角坐标系,
以拱桥的顶点为原点,抛物线的轴为y轴,建立如图所求直角坐标系,设抛物线的方程为x2=-2py(p>0),
∵拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,
∴点(6,-2)在抛物线上,可得62=-2p×(-2),解得p=9
因此抛物线的方程为x2=-18y,
当水面升高1米后,水面所在直线为y=-1,
∴由x2=-18×(-1)=18,得x=±3
| 2 |
| 2 |
故选:A
点评:本题给出实际应用问题,求河水上涨后抛物线形拱桥内部的水面宽度.着重考查了抛物线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
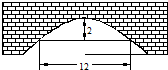 如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是多少米?
如图,抛物线形拱桥的顶点距水面2米时,测得拱桥内水面宽为12米,当水面升高1米后,拱桥内水面宽度是多少米? 如图,抛物线形拱桥的顶点距水面2米时,测得拱 桥内水面宽为12米,当水面升高1米后,则拱桥内水面的宽度为
如图,抛物线形拱桥的顶点距水面2米时,测得拱 桥内水面宽为12米,当水面升高1米后,则拱桥内水面的宽度为 如图,抛物线形拱桥的顶点距水面4m时,测得拱桥内水面宽为16m;当水面升高3m后,拱桥内水面的宽度为
如图,抛物线形拱桥的顶点距水面4m时,测得拱桥内水面宽为16m;当水面升高3m后,拱桥内水面的宽度为