题目内容
在平面内,设A,B为两个不同的定点,动点P满足:
•
=k2(k为实常数),则动点P的轨迹为( )
| PA |
| PB |
| A、圆 | B、椭圆 | C、双曲线 | D、不确定 |
分析:利用平面的数量积运算即可得出轨迹方程.
解答:解:设A(-c,0),B(c,0)(c>0),P(x,y).
则
=(-c-x,-y),
=(c-x,-y).
∵满足:
•
=k2(k为实常数),
∴(-c-x,-y)•(c-x,-y)=k2,
化为x2-c2+y2=k2,
即x2+y2=c2+k2
故动点P的轨迹是原点为圆心,以
为半径的圆.
故选:A.
则
| PA |
| PB |
∵满足:
| PA |
| PB |
∴(-c-x,-y)•(c-x,-y)=k2,
化为x2-c2+y2=k2,
即x2+y2=c2+k2
故动点P的轨迹是原点为圆心,以
| c2+k2 |
故选:A.
点评:本题考查了向量数量积运算、圆的标准方程,属于基础题.

练习册系列答案
相关题目
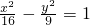 与椭圆
与椭圆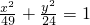 有相同的焦点;
有相同的焦点;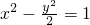 的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条.
的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条.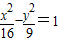 与椭圆
与椭圆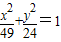 有相同的焦点;
有相同的焦点;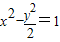 的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条.
的右焦点F作直线l交双曲线于A、B两点,若|AB|=4,则这样的直线l有且仅有3条.