题目内容
一名大学毕业生到某单位应聘,需进行书面测试,要求按顺序完成6道相互独立的题,这名大学毕业生正确做出每一道题的概率都是
.
(Ⅰ)求这名大学毕业生首次做错一道题前,已正确做出了两道题的概率;
(Ⅱ)若这名大学毕业生至少正确做出5道题,才能通过书面测试,求这名大学毕业生通过书面测试的概率.
| 3 | 4 |
(Ⅰ)求这名大学毕业生首次做错一道题前,已正确做出了两道题的概率;
(Ⅱ)若这名大学毕业生至少正确做出5道题,才能通过书面测试,求这名大学毕业生通过书面测试的概率.
分析:(Ⅰ)设“正确解出第i道题”为事件Ai(i=1,2,3,4,5,6),则P(Ai)=
.再根据P(A1A2
)
=P(A1)P(A2)P(
)运算求得结果.
(Ⅱ)记通过书面测试这一关为事件B,而这名大学毕业生至少正确做出5道题,故P(B)=
×(
)5×(
)+
×(
)6,运算求得结果.
| 3 |
| 4 |
. |
| A3 |
=P(A1)P(A2)P(
. |
| A3 |
(Ⅱ)记通过书面测试这一关为事件B,而这名大学毕业生至少正确做出5道题,故P(B)=
| C | 5 6 |
| 3 |
| 4 |
| 1 |
| 4 |
| C | 6 6 |
| 3 |
| 4 |
解答:解:(Ⅰ)设“正确解出第i道题”为事件Ai(i=1,2,3,4,5,6),则P(Ai)=
.
∴P(A1A2
)=P(A1)P(A2)P(
)=
×
×
=
.….(6分)
(Ⅱ)记通过书面测试这一关为事件B,而这名大学毕业生至少正确做出5道题,
即正确做出5道题或6道题才能通过书面测试,故P(B)=
×(
)5×(
)+
×(
)6=
.….(11分)
答:(Ⅰ)中所求概率为
,(Ⅱ)中所求概率为
.…(12分)
| 3 |
| 4 |
∴P(A1A2
. |
| A3 |
. |
| A3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 9 |
| 64 |
(Ⅱ)记通过书面测试这一关为事件B,而这名大学毕业生至少正确做出5道题,
即正确做出5道题或6道题才能通过书面测试,故P(B)=
| C | 5 6 |
| 3 |
| 4 |
| 1 |
| 4 |
| C | 6 6 |
| 3 |
| 4 |
| 2187 |
| 4096 |
答:(Ⅰ)中所求概率为
| 9 |
| 64 |
| 2187 |
| 4096 |
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,属于中档题.

练习册系列答案
相关题目
 .
.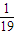 .
.