题目内容
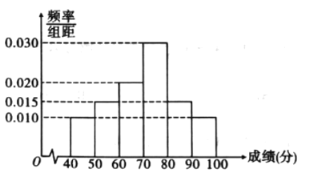
【题目】某市为了增强民众防控病毒的意识，举行了“预防新冠病毒知识竞赛”网上答题，随机抽取
人，答题成绩统计如图所示.
（1）由直方图可认为答题者的成绩
服从正态分布
，其中
，
分别为答题者的平均成绩
和成绩的方差
，那么这名答题者成绩超过
分的人数估计有多少人？（同一组中的数据用该组的区间中点值作代表）
（2）如果成绩超过
分的民众我们认为是“防御知识合格者”，用这名答题者的成绩来估计全市的民众，现从全市中随机抽取
人，“防御知识合格者”的人数为
，求
.（精确到
）
附：①
，
；②
，则
，
；③
，
.
【答案】（1）1587人；（2）
.
【解析】
（1）根据加权平均数公式计算
，根据正态分布的对称性计算
，再估计人数；
（2）根据二项分布的概率公式计算
．
（1）由题意知：
，
依题意
服从正态分布
，其中
，
，
，
服从正态分布
，
而
，
．
成绩超过84.8的人数估计为
人．
（2）成绩超过
分的概率为
．
由题知
，
．
【题目】为考察某种药物预防疾病的效果，进行动物试验，调查了 105 个样本，统计结果为：服药的共有 55 个样本，服药但患病的仍有 10 个样本，没有服药且未患病的有 30个样本.
（1）根据所给样本数据完成 
列联表中的数据；
（2）请问能有多大把握认为药物有效？
(参考公式：
独立性检验临界值表
概率 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
患病 | 不患病 | 合计 | |
服药 | |||
没服药 | |||
合计 |
【题目】为了调查某校高二学生的身高是否与性别有关，随机调查该校64名高二学生，得到2×2列联表如表：
男生 | 女生 | 总计 | |
身高低于170cm | 8 | 24 | 32 |
身高不低于170cm | 26 | 6 | 32 |
总计 | 34 | 30 | 64 |
附：K2
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
由此得出的正确结论是（ ）
A.在犯错误的概率不超过0.01的前提下，认为“身高与性别无关”
B.在犯错误的概率不超过0.01的前提下，认为“身高与性别有关”
C.有99.9%的把握认为“身高与性别无关”
D.有99.9%的把握认为“身高与性别有关”
