题目内容
已知F2(-2,0),F2(2,0),点P满足||PF1|-|PF2||=2,记点P的轨迹为E.
(1)求轨迹E的方程;
(2)若过点F2的直线l交轨迹E于P、Q两不同点.设点M(-1,0),问:当直线l绕点F2转动的时候,是否都有
•
=0?请说明理由.
(1)求轨迹E的方程;
(2)若过点F2的直线l交轨迹E于P、Q两不同点.设点M(-1,0),问:当直线l绕点F2转动的时候,是否都有
| MP |
| MQ |
分析:(1)由F2(-2,0),F2(2,0),点P满足||PF1|-|PF2||=2,知c=2,a=1,b2=3,由此能求出点P的轨迹E的方程.
(2)若l的斜率存在,设l的方程为:y=k(x-2),由
,得:(3-k2)x2+4k2x-4k2-3=0,由l与曲线交于不同点P,Q,知
,由此入手导出
•
=0;若直线l的斜率存在,则P(2,3),Q(2,-3),M(-1,0),故
•
=0成立.所以当直线l绕点F2旋转时,均有
•
=0得到结论.
(2)若l的斜率存在,设l的方程为:y=k(x-2),由
|
|
| MP |
| MQ |
| MP |
| MQ |
| MP |
| MQ |
解答:解:(1)∵F2(-2,0),F2(2,0),点P满足||PF1|-|PF2||=2,
∴c=2,a=1,b2=3,
∴点P的轨迹E的方程为:x2-
=1.
(2)①若l的斜率存在,设l的方程为:y=k(x-2),
由
,消y得:(3-k2)x2+4k2x-4k2-3=0,
∵l与曲线交于不同点P,Q,
∴
,
设P(x1,y1),Q(x2,y2),则x1+x2=
,x1x2=
,
y1y2=k2[x1x2-2(x1+x2 )+4],
∵M(-1,0),
∴
•
=(x1+1,y1)•(x2+1,y2)
=(k2+1)x1x2-(2k2-1)(x1+x2)+1+4k2=0.
②若直线l的斜率存在,则P(2,3),Q(2,-3),M(-1,0),
∴
•
=0成立,
故当直线l绕点F2旋转时,均有
•
=0.
∴c=2,a=1,b2=3,
∴点P的轨迹E的方程为:x2-
| y2 |
| 3 |
(2)①若l的斜率存在,设l的方程为:y=k(x-2),
由
|
∵l与曲线交于不同点P,Q,
∴
|
设P(x1,y1),Q(x2,y2),则x1+x2=
| 4k2 |
| k2-3 |
| 4k2+3 |
| k2-3 |
y1y2=k2[x1x2-2(x1+x2 )+4],
∵M(-1,0),
∴
| MP |
| MQ |
=(k2+1)x1x2-(2k2-1)(x1+x2)+1+4k2=0.
②若直线l的斜率存在,则P(2,3),Q(2,-3),M(-1,0),
∴
| MP |
| MQ |
故当直线l绕点F2旋转时,均有
| MP |
| MQ |
点评:本题考查轨迹方程的求法,探索当直线绕点转动的时候,是否都有向量的数量积为零.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 •
•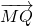 =0成立?若存在,求出实数m的值;若不存在,请说明理由.
=0成立?若存在,求出实数m的值;若不存在,请说明理由. •
• =0成立?若存在,求出实数m的值;若不存在,请说明理由.
=0成立?若存在,求出实数m的值;若不存在,请说明理由. •
• =0?请说明理由.
=0?请说明理由.